Podemos oir la forma de un tambor?

En 1996, Mark Kac [6] propuso la siguiente pregunta: se puede oir la forma de un tambor? O sea, una región  del plano es determinada por el espectro del Laplaciano en  ? La respuesta es NO, y las siguientes dos regiones dan un contraejemplo:

Antes que todo, observemos que las regiones no son isométricas, lo que en el plano significa que no podemos sobreponer una a la otra. Resta ver que son isoespectrales. La demostración de que esas dos regiones son isoespectrales es bien simple e ingeniosa. Se divide la región  en 7 triángulos isósceles denominados A,  , G, como en la figura. Considere  una auto-función de  en  , esto es,  . Es claro que f restricta a alguno de los triángulos es una auto-función sobre ese triángulo. Es más, si tomamos f sobre dos triángulos cualesquiera, por ejemplo F y A, y definimos g sobre un triângulo congruente T como siendo la suma F+A de los valores de f sobre F con los valores de f sobre A, g será una auto-función asociada al auto-valor  :

Lo mismo, naturalmente, valdrá para sumas y diferencias arbitrárias entre los ``pedazos''. Así, la función g definida en  como muestra la figura:

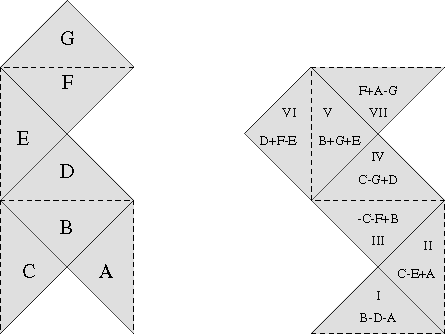
será una auto-función asociada a  en cada triángulo. Resta verificar que g ``se pega''  entre un triángulo y otro, y que  .

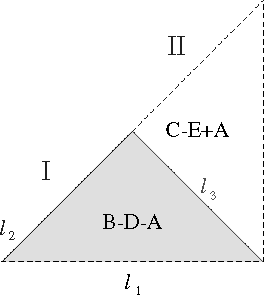
Vamos a mostrar explícitamente la verificación para el paso entre los triángulos I y II:

en  :

B=D donde B-D=0. Como A=0, tenemos que B-D-A=0.

en  :

B=A donde B-A=0. Como D=0, tenemos que B-D-A=0.

en  :

el paso de B apra C es  (ver  ), asícomo -D para -E. Como -A=0 en  , el paso para A, por reflexión, también es  .

Cómo se encontraron estos tambores?

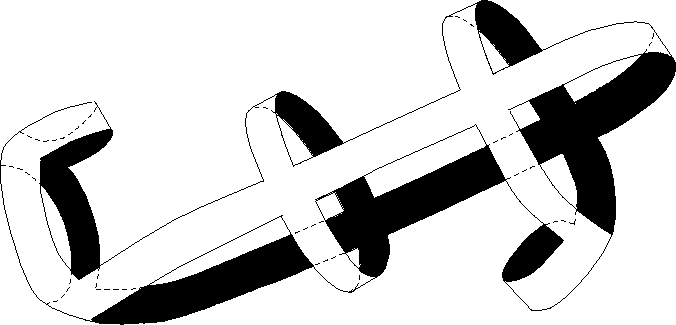
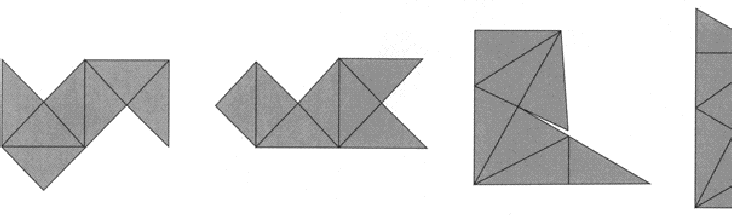
En [1], Buser contruye dos superficies isoespectrales no planas, representadas en la figura:

A partir de ellas, esencialmente cortándolas al medio y ``aplastándolas'' en el plano, C. Gordon , D. Webb y S. Wolpert [5] contruyeron la primera versión de tambores diferentes e isoespectrales:

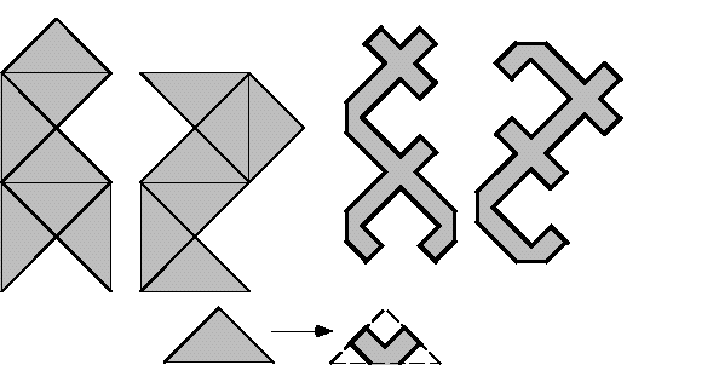
La demostración de que esas regiones montadas con media-cruzes son isoespectrales es esencialmente la misma que dimos para las regiones montadas contriángulos (el lector puede verificar que ella se aplica). En verdad esta demostración fue hecha originalmente para las versiones media-cruz de los tambores [8]. Observándose que la prueba no depende del formato exacto de la pieza fundamental que genera las regiones, sino principalmente de la forma como se pegan esatas piezas, se puede construir diversos tambores diferentes simplemente usando piezas fundamentales diferentes.

Lo que nos resta hacer es contruir las variedades de Buser. En [7], Sunada demuestra el siguiente teorema

Teorema.[Sunada]

Sea G un grupo finito actuando libremenet e isométricamente en una variedad riemanniana compacta M. Suponga que  y  sean subgrupos de G tales que cada clase de conjugación [g] en G intersepte  y  en el mismo número de elementos, i.e.

Entonces  y  son isoespectrales.

Buser usa ese teorema para el grupo G=SL(3,2) de las matrices  invertíbles con coeficientes en  . Los subgrupos son:

Antes de todod, verifiquemos que esos subgrupos satisfacen las hipótesis del teroema de Sunada.

Podemos pensar en  como el subgrupo de las matrices que preservan  . Así,  síy sólo si  tiene a  como auto-vector (auto-valor 1). Esto es, síy solamente si  es auto-vector de g. Como  puede asumir cualquier valor en G,  depende solamente de cuantos autovectores tiene g. Así, [g] y  interseptan  en el mismo número de elementos. pero es fácil ver que el automorfismo  lleva  exactamente en  , portanto  intersepta  tantas veces cuanto [g] intersepta  . Como  es un grupo,

Ahora note que

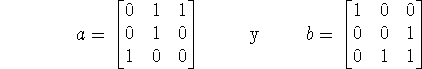
generan G.

Vamos a considerar  , el gráfico de Cayley de G, con generadores a, b. El grupo G actúa en  de forma natural y vamos a considerar los gráficos  y  . Para entender esos gráficos, vamos a estudiar las clases laterales de  y  .

Considere o conmutador

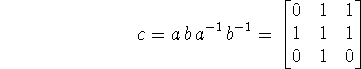
Ese elemento tiene orden 7 y  si y sólo si   (mod 7), por tanto las clases laterales  son disjuntas para diferentes (mod 7) valores de k (ver apéndice). Además, los  cubren todo G, por tanto para cada k existirá un único exponente  tal que  (ver apéndice). Análogamente, hay un único  tal que  . Esos exponentes nos dicenque, en el gráfico  , el elemento representado por  es llevado a  cuando es multiplicado por a. Cuando es multiplicado por b, va a  . Así, basta conocer  y  para construir los gráficos  . Damos abajo tabla que define  y  (ver apéndice):
 

k	0	1	2	3	4	5	6
	3	1	6	0	5	2	4
	0	2	5	6	3	1	4
	1	6	5	0	4	2	3
	0	4	5	1	3	6	2

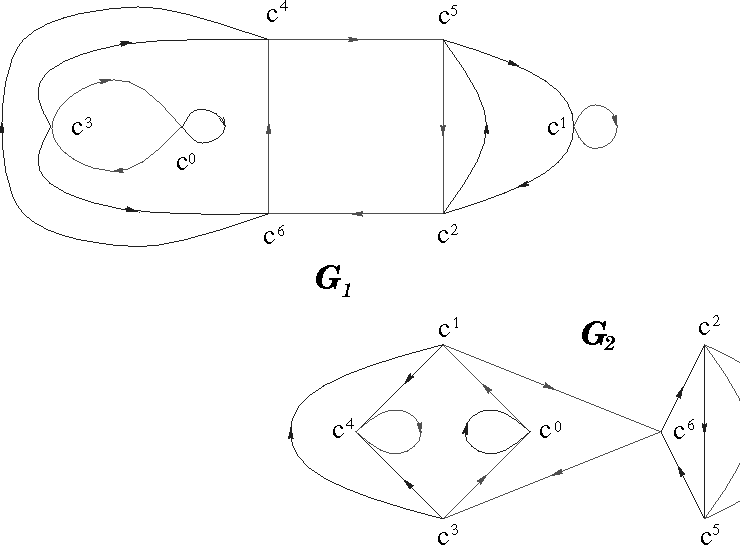
A partir de las tablas es fácil construir los gráficos. Por ejemplo,  tiene 7 elementos, representados por  y que están denominados por k. Las flechas contínuas representan el producto por a y las líneas punteadas, el producto por b. La tabla dice que  . Así, el producto de a por el vértice 5 debe dar el vértice 2.

Así, tenemos bien estudiado el grupo G, sus subgrupos  y  y los cocientes  ,  . Pero cuál será la variedade M que necesitamos para aplicar el teorema de Sunada? Vamos a asociar a cada vértice g del gráfico de Cayley  de G, una cruz con los segmentos del borde denominados como en la figura.

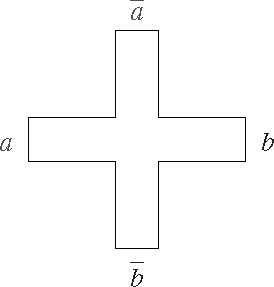
FIGURA 8.

Después identificarempos dos puntas de dos cruces en el siguiente caso: si  , identificamos el borde a de la cruz asociada a  con el borde  de la cruz asociada a  . Análogamente, para  , identifícase b de la primera cruz con  de la segunda.

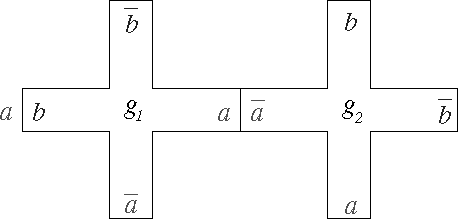
Es claro que cada borde a,  , b ó  de cada cruz estará identificada algún otro borde. Sea M la variedad resultante de estas identificaciones. Cada  lleva la cruz  en la cruz  isométricamente de forma natural. Así, G actúa libremente e isométricamente en M y por tanto, por el teorema de Sunada,  y  son isoespectrales. Las variedades  y  pueden ser visualizadas a partir de los gráficos  y  . Basta hacer el mismo collage de cruces para  y tendremos variedades cociente isoespectrales y claramente no isométricas. Esas variedades, entretanto, no pueden ser colocadas isométricamente en el plano, no son ``tambores''. Si pegamos la ``mitad'' de cada una de ellas, cortando a lo largo de las líneas indicadas en la figura:

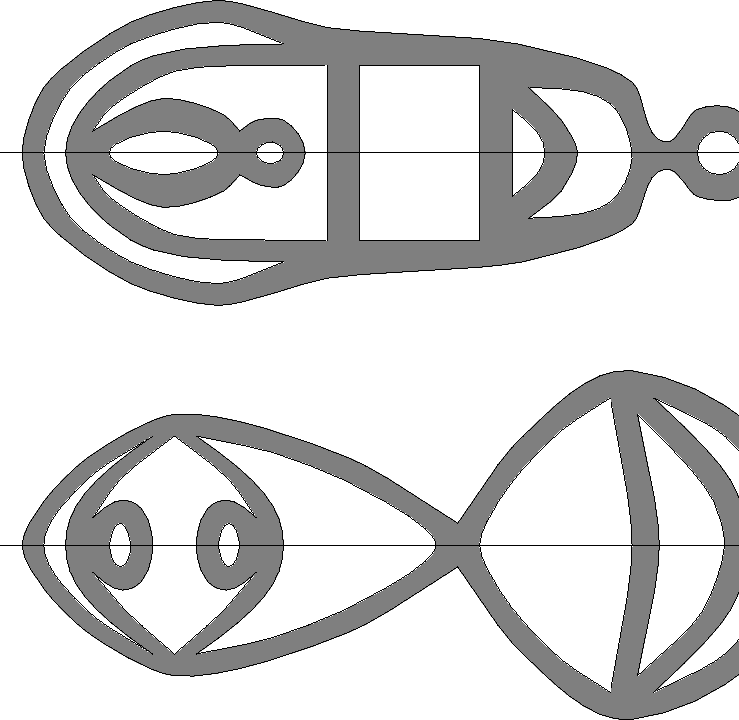
tendremos entonces dos figuras formadas por 7 media-cruces, que pueden se incrustadas isométricamente en el plano dando ``tambores'' satisfactorios.

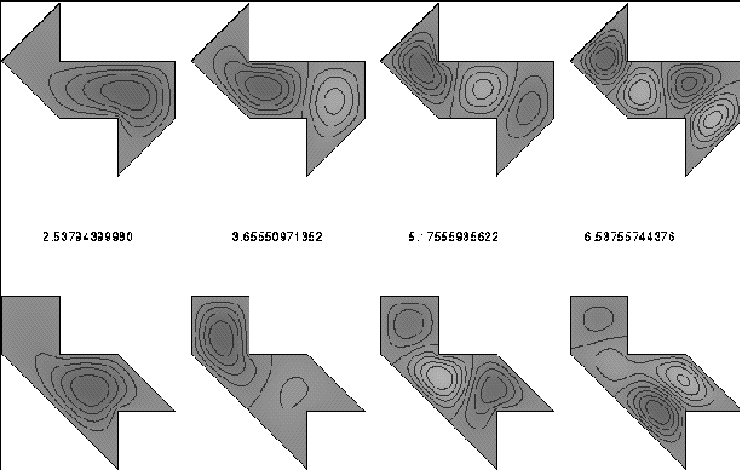
Como ya dijimos, esos dos tambores son, esencialmente, los mismos que presentamos en el inicio del texto.

Apéndice.

Demostraremos aquíalgunas propidades de SL(3,2) que usamos para la construcción de los gráficos  y  . Primeramente, verifiquemos que, si  para  , entonces  , donde  y portanto   (mod 7). Así, las clases laterales de  son disjuntas.

Seguimos esrcibiendo explícitamente algunos elementos de G:

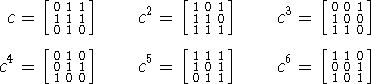
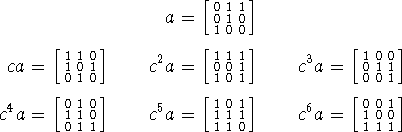
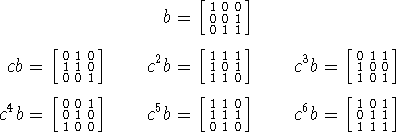
Verificamos por las lista que la única potencia  del conmutador  que pertenece a  ó  es  .

También es fácil ver que  tiene 24 elementos. Existen 8 vectores en  . Podemos llenar las dos columnas libres de un elemento de  de  formas diferentes: en la primera columna vacante podemos colocar cualquiera de los 6 vectores diferentes del nulo y de  , la primera columna. En la tercera, podemos colocar culaquier vector que no sea uno de los dos ya excluídos, o el escogido para ocupar la segunda columna, o la suma de la primera columna con la segunda, esto nos da 4 opciones para llenar la última columna. Como  y  son isomorfos, ambos tienen 24 elementos.

Ya vimos que las clases laterales  son todas distintas. Por tanto la unión de ellas totaliza los  elementos de G, esto es, cubren todo G. Lo mismo se aplica a  .

Vemos, a seguir, cómo construir la tabla de las funciones  y  .

Vamos a comenzar construyendo la tabla de  . Vamos a hacerla al contrario: achar qué k debe ser llevado en un dato  . Necesitamos consultar las listas de  y  . Queremos estudiar la relación entre k y n tales que  . Note que  lleva algún vector  en el vector  , invariante por los lelementos de  . Es decir, todo elemento de  llevará x en  . Basta verificar en la lista de los  cuál elemento hace esto (es claro que por el estudio que hicimos de las clases laterales que hay uno y sólo un tal elemento). Asítendremos  .

Por ejemplo, tomando n=2, buscaremos k tal que  . Hallando la solución x de  , tenemos:

Verificamos en la lista que el elemento  que lleva x en  es ca:

Abajo representamos la lista de todos los  y los respectivos  . Notemos que lo mismo puede ser aplicado a los  .

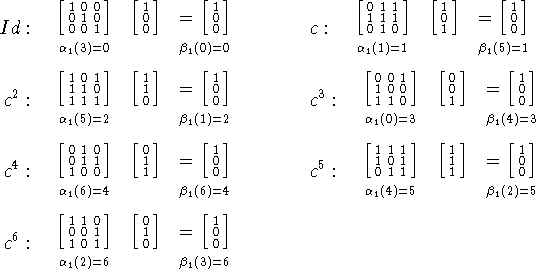
Hallar  y  es más fácil. El subgrupo  está formado por las matrices que preservan el plano  . De forma análoga a lo que hicimos arriba para  , podemos estudiar  . Así, debemos preguntarnos qué espacio es llevado a  por  . Esto es, cuáles on los vectores cuya imágen por  tiene primera coordenada 0. Ese espacio deberá ser llevado por  en símismo, o sea, la imágen deberá tener primera coordenada 0. Es fácil ver que para que pase eso es necesario que las primeras líneas de  y  sean iguales. Por ejemplo, tomemos n=2:

Esto es, los vectores con primera y última coordenadas iguales son llevados en el subespacio invariante por  , por tanto  debe llevarlos en los vectores con primera coordenada 0. Es claro que la primera línea de  debe ser  , la primera línea de  . Como el único  con esta línea es  , tendremos que  .

Haciendo lo mismo con todos los n:

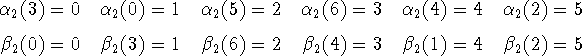
Esto completa la construcción de la tabla de productos en  .