'The Best Card Trick Ever!' printed from http://nrich.maths.org/
Show menu
You will need an assistant and a witness and an ordinary deck
of cards.
Allow the witness to choose (or select) a hand of any five cards and pass them to your assistant, without you seeing them.
Your assistant will give you four of the five cards one at a time and you will be able to tell the witness exactly which card is left in your assistant's hand.
How it works
The first important decision is which of the five cards remains hidden. With five cards in your hand, there will be two of the same suit. Adopt the strategy that the first card your assistant shows you is of the same suit as the card that stays hidden.
Once you see the first card, there are only twelve choices for the hidden card (13 cards in a suit and you have been shown one already).
Now by using the number of arrangements of the remaining three cards the assistant can give you any number from 1 to 6 (there are 3! = 3 x 2 x 1 = 6 arrangements of the three cards)
How do you know which arrangement is which?
Each card has a value so you can label the three cards lowest (l), middle (m) and highest (h). There is a slight problem here if you have two or more cards of the same value (say 5). However you can overcome this by "ranking" the suits. For example clubs (c) are lower than diamonds (d) are lower that hearts (h) are lower than spades (s) (alphabetical order).
This would mean that you can order all the cards in a pack:
Ace-c, Ace-d, Ace-h, Ace-s, 2-c, 2-d, 2-h, 2-s, 3-c, 3-d?
This now means that the assistant can give you cards in an agreed order to represent each of the numbers 1 to 6.
So you could choose the convention:
Allow the witness to choose (or select) a hand of any five cards and pass them to your assistant, without you seeing them.
Your assistant will give you four of the five cards one at a time and you will be able to tell the witness exactly which card is left in your assistant's hand.
How it works
The first important decision is which of the five cards remains hidden. With five cards in your hand, there will be two of the same suit. Adopt the strategy that the first card your assistant shows you is of the same suit as the card that stays hidden.
Once you see the first card, there are only twelve choices for the hidden card (13 cards in a suit and you have been shown one already).
Now by using the number of arrangements of the remaining three cards the assistant can give you any number from 1 to 6 (there are 3! = 3 x 2 x 1 = 6 arrangements of the three cards)
How do you know which arrangement is which?
Each card has a value so you can label the three cards lowest (l), middle (m) and highest (h). There is a slight problem here if you have two or more cards of the same value (say 5). However you can overcome this by "ranking" the suits. For example clubs (c) are lower than diamonds (d) are lower that hearts (h) are lower than spades (s) (alphabetical order).
This would mean that you can order all the cards in a pack:
Ace-c, Ace-d, Ace-h, Ace-s, 2-c, 2-d, 2-h, 2-s, 3-c, 3-d?
This now means that the assistant can give you cards in an agreed order to represent each of the numbers 1 to 6.
So you could choose the convention:
l+m+h = 1
l+h+m = 2
m+l+h = 3
m+h+l = 4
h+l+m = 5
h+m+l = 6
You now know the suit and your assistant can give you any one
of six numbers - but you need a way of distinguishing 12
numbers so six isn't enough! What else can your assistant tell
you?
A pair of cards of the same suit
You and your assistant have a pair of cards of the same suit.
The value (rank) of these cards are two of the numbers from 1
to 13 (Ace to 10, Jack, Queen, King), and these can be arranged
in a circle (like a clock that goes from 1 to 13 instead of 1
to 12). It is now always possible to add a number between 1 and
6 to one card and obtain the other; this amounts to going
around the circle in a clockwise direction with the number 1
being "one more" than 13 (because once you get to 13 (king) you
start again at 1 (Ace)). So, on this clock 3 is four away from
the queen (12) and 7 is four away from 3
In summary, your assistant can show you one card and transmit a
number from 1 to 6. You then add that value to the rank of the
card you have been given first, and leave the suit unchanged,
thus identifying the hidden card. It is therefore not only
necessary for your assistant to give you a card of the same
suit but they must give you the card to which you will add a
number from 1 to 6 to get the card the assistant has (based on
this clock, or modular arithmetic).
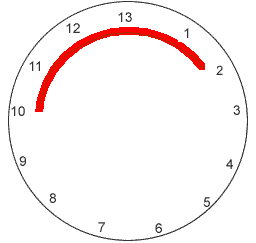
Say the two cards are 2 and 10. Your assistant must give you the 10 and the number 5 because 10 + 5 = 2 in mod 13. The difference between 2 and 10 is eight and your assistant cannot "send 8 to you".
Examples:
If we are dealt 3S, 5S, 3D, 4C, 9H, place 3S down first (to
indicate that the secret card is a spade), then 3D, 9H, 4C
(low, high, middle, to indicate that the secret card is 2 more
than the 3S).
If we are dealt 3S, 9S, 3D, 4C, 9H, place 3S down first (to
indicate that the secret card is a spade), then 9H, 4C, 3D
(high, middle, low, to indicate that the secret card is 6 more
than the 3S).
If we are dealt 3S, 10S, 3D, 4C, 9H, place 10S down first (to
indicate that the secret card is a spade), then 9H, 4C, 3D
(high, middle, low, to indicate that the secret card is 6 more
than the 10S).
If we are dealt 2H, JH, 4D, 4C, 4S, place JH down first (to
indicate that the secret card is a heart), then 4D, 4S, 4C
(middle, high, low, to indicate that the secret card is 4 more
than the JH).
* This trick first appears in Wallace Lee's book "Math
Miracles" in which he credits its invention to William Fitch
Cheney, Jr., a.k.a. "Fitch."
A .pdf file of the original article, the first part of which describes the trick, is available on Michael Kleber's web page, at http://people.brandeis.edu/~kleber/Papers/card.pdf
A .pdf file of the original article, the first part of which describes the trick, is available on Michael Kleber's web page, at http://people.brandeis.edu/~kleber/Papers/card.pdf
