Ing. Alonso Ramírez Manzanares. CIMAT.
Reporte e Investigación del método Mean Shift, descripción del mismo y aplicaciones a Filtrado preservando bordes, Segmentación y Tracking de objetos no rígidos en tiempo Real.
REFERENCIAS
En este trabajo se está revisando una técnica no paramétrica para el análisis de un espacio de características con densidades complejas multimodales llamada Mean-Shift. La utilización de esta técnica se basa en la aplicación recursiva del método para encontrar el punto estacionario más cercano de la función de densidad, ayudando así a encontrar las modas de la misma. Como casos de aplicación se presentan dos tareas de Visión de bajo nivel que son: el filtrado de imágenes preservando bordes y la segmentación, y por otro lado una tarea de Visión de Mediano Nivel que es el Tracking de Objetos no rígidos en tiempo real. En los dos primeros ejemplos un parámetro único debe de ser proporcionado por el usuario y puede trabajarse con imágenes o secuencias de imágenes tanto en color como en escala de grises. El método que se analiza a continuación puede ser utilizado en condiciones en donde la cámara se esta moviendo y en la que una técnica de eliminación del fondo inmóvil no seria suficiente. En lo que respecta a tracking, el módulo central del cálculo, que encuentra la posición mas probable del objetivo en el cuadro actual, se basa en las iteraciones del método de mean-shift. La similitud entre el modelo objetivo y los objetivos candidatos es expresado por una métrica derivada del coeficiente de Bhattacharyya. Se muestran ejemplos en los cuales se ve el amplio desempeño del método y la robustez a oclusiones, "desórdenes" y escalamientos del objetivo.
1.- Introducción
Para las tareas de visión de bajo nivel es necesario que éstas sean controladas eficientemente por un número reducido de parámetros y que puedan representar confiablemente la entrada de datos, logrando de esta manera una fácil interconexión con las tareas de alto nivel.
El análisis basado en el espacio de características puede alcanzar los requerimientos anteriores. Un espacio de características es un mapeo de la entrada obtenida a través del procesamiento de los datos en pequeños subconjuntos cada vez (en el caso del espacio de color estos subconjuntos pueden ser píxeles individuales). Para cada subconjunto una representación paramétrica de la característica es obtenida y mapeada como un punto en el espacio multidimensional del parámetro. En este espacio multidimensional se pueden localizar las características mas significativas o importantes como clusters y la meta de este análisis es poder delinear o separar estos clusters.
La naturaleza del espacio de características es dependiente de la aplicación mientras que el análisis de este espacio es totalmente independiente de la misma. Aunque existen muchas técnicas en la literatura para delinear cluster muchas de ellas no son apropiadas para trabajar con datos reales. Los métodos que presuponen un número fijo de clusters ya sea fijados por el usuario o bien encontrados mediante optimización; así como métodos que presuponen formas fijas para los clusters (normalmente elípticas) tienen problemas para desempeñarse correctamente en un real espacio de características.
Para ver más claro un espacio de características vamos a tomar el ejemplo del mapeo de una imagen a su correspondiente espacio tridimensional de características L*u*v* como se muestra en la siguiente figura:
Figura 1. Una imagen a Color
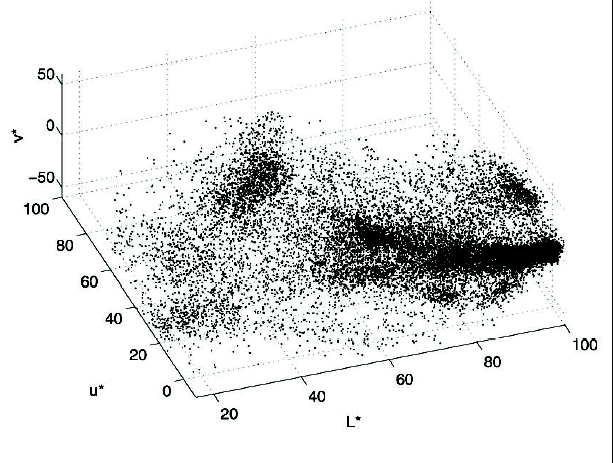
Figura 2.- Mapeo al espacio de características L*u*v*
Como se puede observar, se tiene una relación clara entre los colores dominantes de cada sección de objeto en la imagen y los clusters que se obtienen en el espacio de características. Hay que recordar que el espacio L*u*v* fue diseñado para tener una correspondencia mas uniforme entre distancias geométricas y distancias preceptúales para colores que están bajo la misma referencia de iluminación.
Tratar de imponer un numero de clusters a priori o bien una forma geométrica para los mismos fallará. Los espacios de características que tienen estructuras arbitrarias (como el anterior) solo pueden ser analizados exitosamente por métodos no paramétricos ya que estos métodos no llevan suposiciones en su metodología. Los métodos jerárquicos que dividen o agrupan los datos en base a una medida de proximidad son computacionalmente muy caros y el criterio de paro no tiene una definición clara.
El método que se utiliza en este trabajo es uno perteneciente a hacer detección de clusters por un método no paramétrico basado en el estimador de la densidad. Lo que se hace es que se estima el espacio de características como la función de densidad de probabilidad (p.d.f. probability density function) empírica del parámetro representado. Hecho lo anterior se sabe que las regiones con alta densidad en el espacio de características corresponden a máximos locales en la p.d.f., es decir las modas de la densidad desconocida. Para detectar estas modas se ha utilizado la técnica llamada Mean- Shift. Como se verá durante el desarrollo de este trabajo, resulta que un módulo de análisis del espacio de características puede ser utilizado en varias tareas ya que es una herramienta muy poderosa y versátil.
Se muestra además un método para realizar tracking en tiempo real de objetos no rígidos basados en características como color y/o textura, donde las distribuciones estadísticas identifican el objeto de interés. El método es adecuado para una amplia variedad de objetos con diferentes colores y/o patrones de textura. Las iteraciones de Mean-Shift son empleadas para encontrar el objetivo candidato que es el mas parecido al modelo, y para determinar la similaridad se ha usado una métrica basada en el coeficiente de Bhattacharyya.
2.- Análisis de Mean Shift General
La estimación del Kernel de densidad es el método más popular:
Dados n puntos que son datos xi, i=1,..., n en un espacio d-dimensional Rd, el estimador de densidad multivariada basado en kernel con kernel K(x) y matriz H que es definida positiva y bandada de dimensión dxd está dado por:
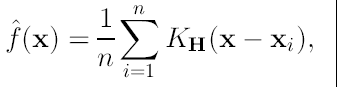(1)
donde:
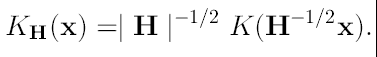(2)
El kernel d-variado K(x) es una función acotada con soporte compacto que satisface las siguientes condiciones:
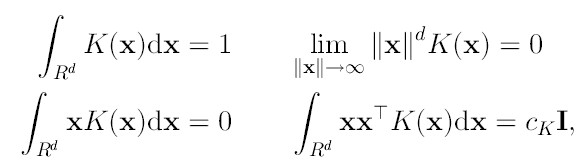(3)
donde cK es una constante. Las condiciones anteriores que se pueden ver como: la integral sobre todo el dominio es 1, la esperanza es 0, se tiene soporte compacto, etc. Ahora bien el kernel multivariado se puede generar de dos diferentes formas:
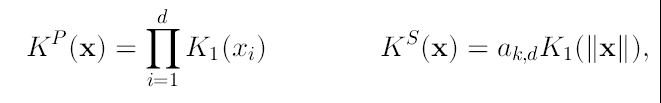(4)
La constante
simplemente asegura que la integral de KS(x) sea 1, aunque esta condición puede ser ignorada en este contexto.
En este caso estamos interesados en los kernels radialmente simétricos como es el caso de KS(x) y en particular un caso especial de kernels que satisfacen:
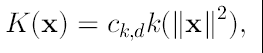(5)
en cuyo caso solo es necesario definir k(x) (que es llamado el perfil del kernel) para valores positivos. La constante de normalización cK,d que hace que K(x) integre a uno, es asumida estrictamente positiva.
Usar una matriz H completamente parametrizada incrementa la complejidad de la estimación, por lo que en la práctica se utiliza H como una matriz diagonal con un único parámetro h, es decir H=h2I, con lo cual reducimos la complejidad del análisis, ya que así solo hay que proporcionar un parámetro h. Pero para poder utilizar esta aproximación es necesario asegurar que se tiene una métrica euclidiana para el espacio de características. Para que esto se vea mas claro agrego la siguiente lámina explicativa:
que dan orígenes a funciones de densidad como:
Si tomamos solo este parámetro, el estimador de densidad con kernel (KDE) tiene la forma:
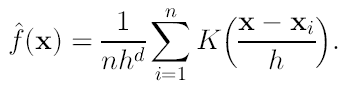(6)
En la práctica se puede probar (mediante el cálculo de AMISE -aproximación a la media del error cuadrático entre la densidad y su estimador-) que ésta medida es minimizada si utilizamos el kernel de Epanechnikov
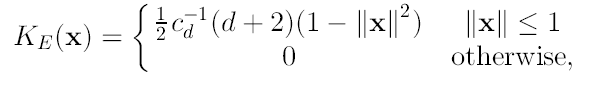(7)
que tiene el perfil:
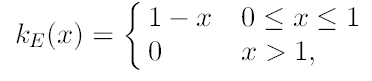(8)
Donde cd es el volumen de la esfera d-dimensional. Aunque también podemos utilizar el kernel normal multivariado:
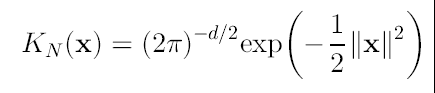(9)
que tiene el perfil:
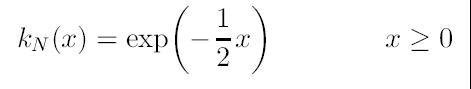(10)
Empleando la notación de perfil, el estimador de densidad se puede escribir como:
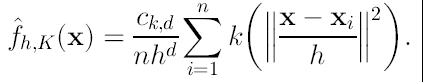(11)
Ahora bien, para hacer el análisis necesitamos localizar las modas de esta densidad, es decir tenemos que encontrar los sitios donde 
.
Explotando la linealidad de (11) y utilizando la regla de la cadena podemos escribir:
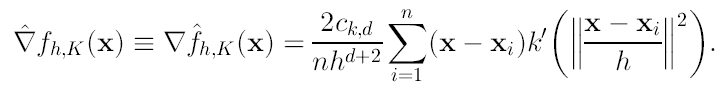(12)
Asumiendo que la derivada del perfil k existe para todo x podemos definir el perfil:
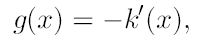(13)
que da origen al kernel:
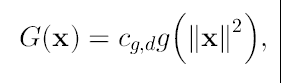(14)
Introduciendo g(x) en (12) nos lleva a:
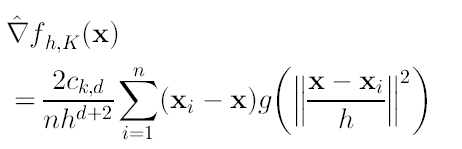(15)
dividiendo y multiplicando dentro de la sumatoria por
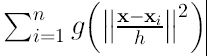(15a)
tenemos:
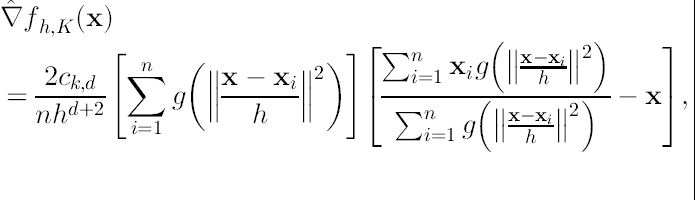(16)
donde 15(a) se asume que es un número positivo, condición que satisfacen los kerneles usados en la práctica.
De la expresión (16) podemos ver que el primer término es proporcional (solo cambian las constantes) al estimador de densidad en el punto x utilizando el kernel G, el cual tiene la expresión:
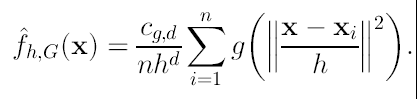(17)
El segundo término de (16) es el vector Mean-Shift.
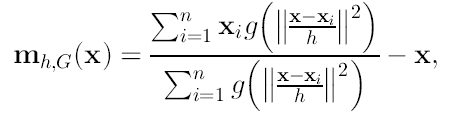(18)
éste término es la diferencia entre la media pesada (donde se está usando el kernel G para los pesos) y x que es el centro del kernel.
de (16), (17) y (18) tenemos que:
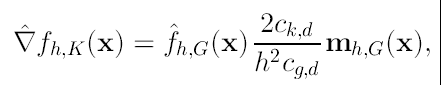(19)
donde despejando nos lleva a:
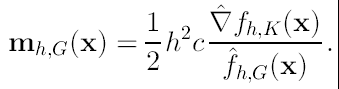(20)
Como podemos ver, el vector Mean-Shift en la posición x calculado con el kernel G es proporcional al gradiente del estimador de densidad obtenido con el kernel K. La normalización está dada por el estimador de densidad con el kernel G en el punto x (el denominador de la expresión). Entonces el vector Mean-Shift es un vector que apunta en la dirección de máximo crecimiento de la densidad. Por lo tanto mediante el cálculo secuencial de este vector y la traslación al punto encontrado para calcularlo nuevamente, nos llevará a los puntos estacionarios de la densidad estimada, es decir a las modas. Quedando entonces el procedimiento como:
Precisamente la normalización anteriormente explicada es la que le da un gran desempeño al algoritmo, pues en donde hay pocos puntos el vector tiene magnitud grande (pues el denominador de normalización es pequeño), por lo tanto se avanza a pasos grandes, lo cual es correcto pues estas zonas de pocos puntos son de poco interés para el análisis del espacio de características. Por el contrario cuando estamos en una zona del espacio con alta densidad de puntos la magnitud del vector es pequeña (ya que el denominador de normalización es grande) y se avanza a pequeños pasos haciendo un análisis mas refinado.
Condiciones suficientes para Convergencia.
Denotemos por {yj}j = 1,2,... la secuencia de posiciones secuenciales del kernel G que tienen la forma:
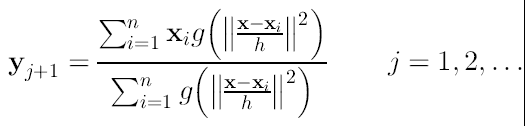(21)
Existe un teorema que se enuncia a continuación:
Teorema 1: Si el kernel K tiene un perfil convexo y monótonamente decreciente, las secuencias {yj}j = 1,2,... y {
} convergen y además {} es monótonamente creciente.
El teorema anterior mantiene su validez si a cada punto xi se le multiplica un peso no negativo wi, esto será de mucha importancia cuando se aplique al problema de tracking. La garantía de convergencia se muestra en la prueba del teorema y es debida a la magnitud adaptiva del vector Mean-Shift, que elimina la necesidad de procedimientos adicionales para seleccionar el tamaño de paso adecuado en cada iteración.
En la implementación con datos discretos, el número de pasos necesarios para la convergencia depende del kernel G utilizado. Cuando G es el kernel uniforme, la convergencia es alcanzada en un número finito de pasos, ya que las localizaciones generando distintos valores de la media es finito. Pero, cuando el kernel G da pesos distintos a los puntos de acuerdo a la distancia al centro del kernel el procedimiento Mean-Shift es infinitamente convergente (por ejemplo cuando usamos el kernel normal), por lo que en este caso es necesario poner una cota mínima de paro para la magnitud del vector.
Las implicaciones del teorema anterior son las siguientes:
La magnitud del vector Mean-Shift converge a cero.
Segundo si una posición de arranque yj esta lo suficientemente cerca de una moda de 
, el algoritmo convergerá a ella.
Por lo tanto, se puede proponer un podado del método de la siguiente forma:
Un punto que es máximo local se define como aquel que es el único punto estacionario en una vecindad definida por una pequeña esfera. El segundo paso se puede realizar si se escoge un vector aleatorio de magnitud pequeña y a partir de ese punto se vuelve a dejar converger el algoritmo. Si el algoritmo converge al mismo punto (mas cerca que una tolerancia dada), entonces es un máximo local, de lo contrario se elimina. La prueba anterior eliminará aquellos puntos estacionarios que se encuentran en zonas "planas" de la distribución. La secuencia del procedimiento se muestra en la figura A.
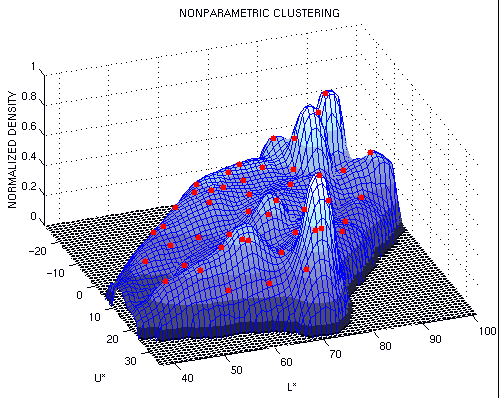
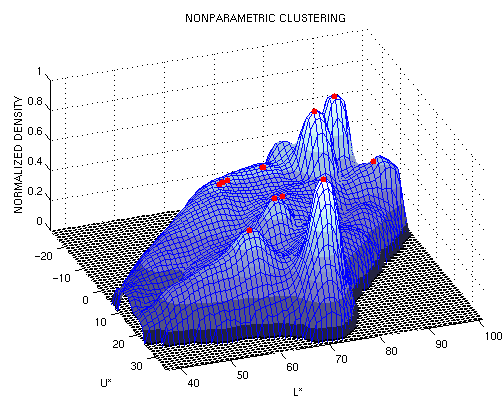
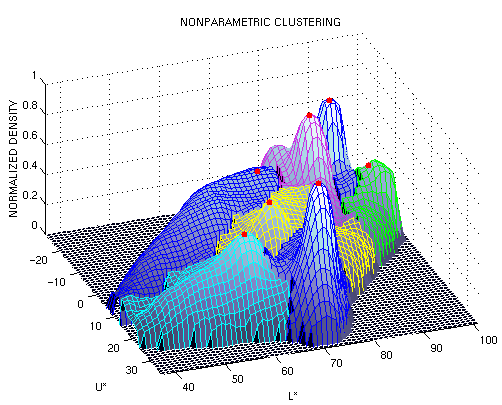
Figura A. Secuencia de localizacion de las modas en un espacio de características. Se hace el procedimiento para todos los puntos, estos convergen a varios puntos estacionarios y finalmente se ejecuta el el podado. Al final se muestran los clusters encontrados, como se puede ver , la naturaleza del método no paramétrico permite cualquier cantidad de clusters, con formas arbitrarias.
La propiedad de tener una trayectoria Suave
Teorema 2: El coseno del ángulo entre 2 vectores consecutivos de Mean-Shift cuando se está utilizando el kernel normal es estrictamente positivo.
Lo anterior nos indica que el ángulo entre 2 vectores consecutivos siempre es menor a 90 grados. Tomando en cuenta lo anterior, parece que el kernel normal es el óptimo a utilizar, pues de esta manera los pasos ascendentes llevan una trayectoria suave y no zigzagueante. Sin embargo en las aplicaciones se ha preferido utilizar el kernel uniforme, porque al usarlo se tiene convergencia finita, aunque cuando se utiliza el kernel normal se obtienen mejores resultados.
3.- Análisis robusto del espacio de características
Antes de hacer el análisis del espacio de características es necesario determinar la métrica del mismo y la forma del kernel, ya que el mapeo de entrada muchas veces deja asociada una métrica no Euclidiana para el espacio.
Siempre puede ser utilizada la distancia de Mahalanobis en el espacio de características (cambiando la matriz H de la ecuación (2) ), pero es recomendable utilizar una distancia Euclidiana, ya que de esta manera un único parámetro h (H=h2I) es empleado en el análisis.
Los puntos de arranque del método deben de ser escogidos de tal forma que se garantice que todo el espacio de características ha sido subdividido y explorado por las ventanas de los kernels. Como las ventanas evolucionan hacia las modas, casi todos los puntos son visitados y por lo tanto toda la información durante la búsqueda es capturada.
Un post-procesamiento puede anular los defectos que se encuentran por el hecho de que el uso de un umbral, para el criterio de paro, puede dar puntos estacionarios que están muy cercanos, siendo que pertenecen a la misma moda, o bien puntos estacionarios que pertenecen a un zona plana de la densidad (donde el algoritmo se detiene por ser el gradiente cercano a cero). El post-procesamiento consiste en fusionar los puntos candidatos que se encuentren a una distancia menor a h, agrupándolos al punto donde la densidad tiene el valor mayor.
Para delinear los clusters se utiliza el hecho de que, el conjunto de puntos visitados que encontraron su punto estacionario en una misma moda, pertenecen al mismo cluster. De lo anterior se puede entender porque es posible delinear clusters con forma arbitraria. Puede darse el caso de que cerca de los límites del espacio, un punto haya sido visitado por mas de una búsqueda, entonces sin ningún problema se puede anular esta ambigüedad, pues se cuenta con la información espacial (punto x ,y de la imagen) sobre la cual podemos aplicar una decisión lógica de a que cluster debemos de asociarlo.
Selección del parámetro h
La selección del parámetro h de manera óptima puede ser visto desde puntos de vista diferente. Existe la motivación estadística la cual nos dice que el parámetro h óptimo es aquel que minimiza la medida AMISE (diferencia cuadrática entre estimador y real) lo cual es poco práctico de calcular, o bien existe la motivación de la descomposición del espacio en clusters, donde el criterio es encontrar una h tal que el número de clusters se mantiene en diferentes experimentos o bien, estudia la interconectividad de los clusters. Pero para nuestros casos de aplicación el parámetro h será aquel que sea establecido por el usuario (o por una tarea de alto nivel) como un parámetro que indica el refinamiento del análisis.
Detalles de implementación
Para que podamos tener una eficiente implementación, necesitamos primero re-muestrear la entrada en una grid regular que es un procedimiento similar a definir un histograma, donde la interpolación lineal es usada para calcular los pesos asociados con los puntos del grid. Por otro lado, cuando se quieren localizar los puntos que caen dentro de un kernel con centro dado, se pueden utilizan algoritmos de búsqueda de ámbito multidimensional, lo cual reducirá considerablemente el tiempo de cálculo.
4.- Aplicación 1: Suavizado de Imágenes preservando bordes
Como se mostrará a lo largo de la descripción de aplicaciones, el análisis del espacio de características en una herramienta independiente que puede ser utilizada para varios propósitos.
Algo muy importante para el mapeo al espacio de características es que las diferencias de color que se perciben deben de corresponder con distancias Euclidianas en el espacio de color, garantizando así, que la segmentación obtenida sea congruente con el objetivo deseado.
La transformación usada en este trabajo fue la L*u*v*, ya que tiene la propiedad de mapeo lineal, siendo mas conveniente que el simple espacio RGB. Tanto en esta aplicación como en la siguiente se ha utilizado un espacio de características ampliado, es decir, las componentes del espacio de color p mas las 2 componentes de localización espacial de cada píxel de la imagen. A esto se le llama dominio empalmado (joint domain). Por ejemplo, en el caso de imágenes en escala de grises p=1, en el caso RGB p=3 y en el caso de imágenes multiespectrales (como por ejemplo las de satélite) p>3. En este nuevo espacio del dominio empalmado se asume la medida Euclidiana. y el nuevo rango espacial es d = p+2, donde la naturaleza diferente de los datos debe de ser compensada con una normalización adecuada. Dado lo anterior, el kernel multivariado es definido como el producto de 2 kernels radialmente simétricos. La medida euclidiana acepta que se tenga un simple parámetro h para cada dominio quedando:
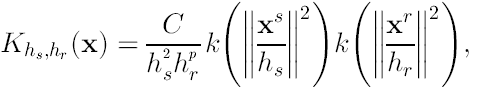(22)
donde xs es la parte espacial y xr es el la parte del espacio de características. Si se utiliza un kernel de Epanechnikov o un kernel normal truncado se obtiene un desempeño satisfactorio. Hay que remarcar que bajo estas condiciones, el usuario solamente debe de indicar el parámetro h=(hs,hr), que al controlar el tamaño de cada kernel, controla la resolución al detectar las modas.
Algoritmo:
Dadas xi y zi, i = 1..n la entrada d-dimensional (dominio empalmado) y la salida de una imagen filtrada respectivamente:
Para cada píxel i:
Los superíndices indican las partes, espacial (s) y del espacio de características (r). El último paso nos indica cómo en la posición xis, se va a almacenar el valor del espacio de características que el método haya detectado como una moda para ese píxel.
Ejemplo: tenemos la famosa imagen de prueba Lena.bmp de dimensiones 256x256 con rango dinámico de 0 a 255. Le agregamos ruido gaussiano con
s =10, y procedemos a aplicarle el método usando un kernel uniforme con los parámetros (hs,hr)=(2,10) obteniendo los resultados mostrados en la figura 3. El procedimiento anterior se realizó utilizando el software proporcionado por los autores "EDISON", en una PC Intel Pentium III a 450 MHz con 256 MB RAM, el tiempo que llevó el proceso fue de 3.32 segundos. El número de modas detectadas por el proceso fue 12,576.
a)Imagen Original
b)Imagen con Ruido
c)Imagen Filtrada
d) Diferencia I=Original-Filtrada
e) Zoom
Figura 3.- Una imagen Filtrada
A manera de demostración, los autores muestran la figura 4, en la cual se puede ver a detalle como se comporta el método. En la figura 4a se muestra una sección de una imagen de prueba en el dominio empalmado, ya que hay información de la escala de gris y de la posición del píxel. En la figura 4b se muestran los caminos seguidos por el procedimiento Mean-Shift en varios píxeles tanto para la zona plana como para la línea blanca de la derecha. En ella se puede ver como los puntos de convergencia de método en la parte plana se localizan en el centro de la zona. La figura 4c nos muestra el resultado de la imagen filtrada con claras zonas quasi-homogéneas.
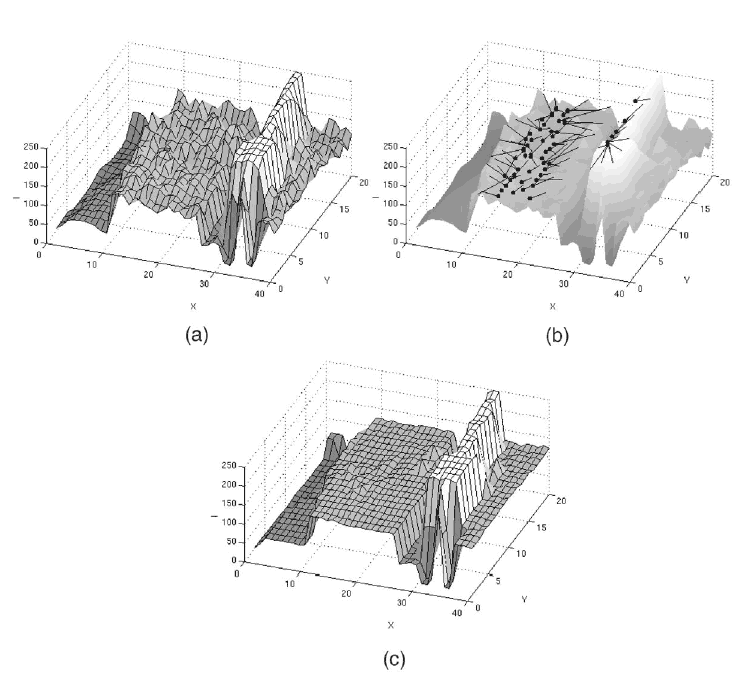
Figura 4.- Procedimiento a detalle
El comportamiento de la figura 4 se puede explicar de la siguiente manera: Si tomamos un píxel de la línea derecha, el kernel uniforme define un paralelepípedo como el mostrado en la figura 5, el cual esta centrado en el píxel en cuestión, y el cálculo del vector Mean-Shift toma en cuenta sólo los píxeles que tienen tanto sus coordenadas espaciales y el valor de escala de gris dentro de este paralelepípedo, entonces si este no es muy grande, solo los píxeles que pertenecen a la línea (los "altos") son los promediados, garantizándose que el nuevo centro del la ventana estará sobre la línea. Basado en lo anterior podemos definir un comportamiento general: si nosotros aumentamos el parámetro hs solo las características de la imagen que tengan un gran soporte espacial serán encontradas en la imagen filtrada, ahora bien si aumentamos el parámetro hr, solo las características con alto contraste de color sobrevivirán. Por lo tanto también es lógico aclarar que si estos parámetros son pequeños, por ejemplo toman tamaño 1, pues la imagen filtrada será idéntica a la original. Otra ventaja de lo intuitivo de estos parámetros es que para imágenes que mantienen las mismas estructuras espaciales se puede fijar el parámetro hs y manipular solamente el hr, y lo inverso para imágenes que mantienen características similares en cuanto su contraste de color.
Figura 5.- El alcance de un kernel como paralelepípedo
5.- Aplicación 2: Segmentación de Imágenes
La segmentación de imágenes se puede definir como la descomposición de la imagen en regiones homogéneas, que compartan ciertas características. Esta aplicación (ya sea tanto de color como de escala de grises) es una lógica ampliación del método de filtrado preservando bordes. El algoritmo es similar, solamente que en este caso se va a hacer un "podado" de todas las modas encontradas dejando solo aquellas que son significativas, y todos los píxeles que se encuentren dentro de una vecindad cercana a alguna de estas modas significativas en el dominio de densidad empalmada, serán asociados a ellas, generando así las zonas homogéneas.
Algoritmo:
Dadas xi y zi, i = 1..n la entrada d-dimensional (dominio empalmado) y la salida de una imagen filtrada respectivamente, con Li la etiqueta del i-ésimo píxel en la imagen segmentada.
El paso b) donde se encuentran los clusters, puede ser modificado y mejorado utilizando para ello la información a priori que tengamos sobre las regiones, o bien el modelo físico de la segmentación que deseamos. El autor menciona que dado que este proceso se realiza en regiones gráficamente adyacentes, usar técnicas iterativas puede acelerar considerablemente el algoritmo.
El autor compara el desempeño con algoritmos tales como "representación de masa" (blob representation), técnicas de cluster jerárquicas, métodos con campos aleatorios markovianos, llegando a la conclusión de que su método es mejor. Lo anterior fijándose en características como tiempo de ejecución y resultados en superficies con textura (como por ejemplo el cielo).
Ejemplo 1: Tomamos una imagen de la hermosa zona arqueológica de Chichen Itza 307x205 píxeles a 16 millones de colores. Utilizando los parámetros (hs,hr)=(8,13) y M = 40, obtenemos los resultados mostrados en la figura 6.
b) Filtrada
c) Segmentada
d)Bordes
Figura 6.- Proceso de segmentación aplicado a una imagen de prueba.
Desde el punto de vista de usuario, es relativamente fácil encontrar los parámetros para alguna tarea en específico, por ejemplo en este caso se buscó específicamente poder segmentar el cielo en una sola región, lo cual se logró cambiando los parametros de 4 a 5 veces. El tiempo que se llevó la segmentación es de 15 segundos y 13 centésimas, lo cual incluye la lectura de entrada, la escritura de las 3 imágenes de resultado, la detección de las modas (4163 en este ejemplo), el agrupamiento de estas para la segmentación y el podado del número mínimo de píxeles M para determinar una región, quedando al final 63 regiones.
6.- Aplicación 3: Tracking en tiempo real de objetos no rígidos
A continuación se hace un planteo del problema de tracking para poder aplicar el método de mean-shift.
La característica z que representa al objeto objetivo, ya sea tanto color o textura, tiene la densidad de probabilidad qz, y el objetivo candidato centrado en la posición y tiene la característica distribuida de acuerdo a pz(y), siendo entonces el problema encontrar la posición discreta y en la cual su densidad asociada pz(y) es la más similar a qz. Para poder definir que tan parecida es una densidad a la otra, lo más lógico sería usar el error de clasificación de Bayes, ya que como es sabido, entre mas grande sea este error son mas parecidas las densidades, ya que hay mas ambigüedad al elegir a cual de las densidades pertenece una clasificación (un ejemplo intuitivo se muestra en la figura 7). Es entonces necesario maximizar con respecto a y el error de Bayes para la densidad del modelo y la del objetivo, asumiendo por el momento que el objetivo tiene igual probabilidad a priori de aparecer en cualquier posición y.
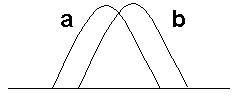
a) Error de Clasificación de Bayes grande, las densidades son muy parecidas
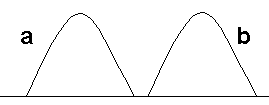
b) Error de Clasificación de Bayes pequeño, las densidades son muy diferentes.
Figura 7. Ejemplo intuitivo de la relacion entre el Error de Bayes y similitud de densidades.
Aquí es donde aparece el coeficiente de Bhattacharyya, ya que esta muy relacionado al error de Bayes (es proporcional), siendo su ventaja que es computacionalmente barato de calcular. La forma general esta dada por:
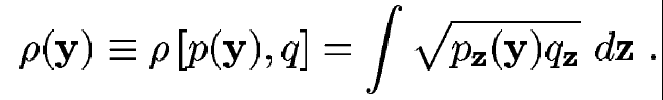(23)
Se sabe que dados unos conjuntos de parámetros a , b (que pueden ser media, varianza, numero de modas, etc ) de las distribuciones p y q, si la evaluación de (23) da un valor menor para el conjunto a que cuando se utiliza b , entonces existen una probabilidades a priori para p y q tales que el error de Bayes para el conjunto a es mayor que para el conjunto b .
En este trabajo se usan los histogramas (en 1D o en 3D en el caso de color) como un estimador de densidad no paramétrico, y aunque no es definitivamente el mejor, si es muy rápido de calcular. Entonces se ha estimado la densidad discreta como:
(24)
(25)
con:
(26)
formando un histograma de m entradas. Entonces el estimador muestral del coeficiente de Bhattacharyya esta dado por:
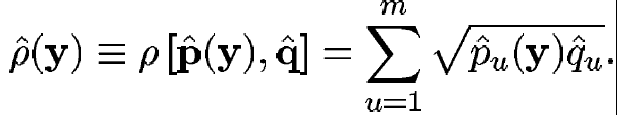(27)
Ahora bien, podemos utilizar una medida de distancia entre las 2 distribuciones basados en (27) quedando como:
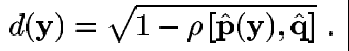(28)
donde se puede probar que (28) es una distancia, pues cumple con todos los requerimientos para serlo. La distancia anterior está bien utilizada ya que es cercana a la óptima por su relación al error de Bayes, tiene toda la estructura de una medida y además usando densidades discretas tenemos invarianza ante escalamientos, es decir si nuestro objetivo mide 200 píxeles y la mitad de ellos son negros y la mitad blancos, conserva la misma densidad discreta si solo mide 50 píxeles y nuevamente la mitad son negros y la mitad son blancos, ya que los histogramas están normalizados como se muestra en (26).
Algoritmo de tracking
Para que el algoritmo de tracking esté completo se asume que ya se cuenta con un procedimiento que marca de manera óptima el objetivo a ser "trackeado" en el frame inicial y otro que hace un análisis periódico de cada objeto detectando posibles actualizaciones del modelo objetivo, debido a cambios radicales en color, los cuales pueden darse por condiciones de iluminación.
Patrón Objetivo. Vamos a definir{xi*} i=1..n, como todos los píxeles que componen al modelo objetivo, es decir la zona que es marcada como el objeto a hacer tracking, estos puntos están centrados en 0. Definimos también la función b que va de R2
® {1..m} la cual asocia a cada píxel en la posición xi* el índice b(xi*) del histograma (el bin). Entonces la probabilidad de encontrar el color u en el modelo objetivo es derivada empleando un kernel decreciente monótonamente con perfil k, que realmente lo que hace es asignar un peso pequeño de probabilidad a los píxeles que se encuentran lejos del centro del kernel, y lo contrario para los píxeles que están cercanos al centro, esto hace mas robusto el análisis, pues los píxeles que están mas alejados del centro del objetivo son los mas propensos a desaparecer cuando se tienen oclusiones o al rotar en el fondo. El radio del kernel anterior es tomado igual a 1, ya que se asume que las coordenadas x,y de los píxeles han sido normalizadas para que un factor horizontal hx y uno vertical hy estén a una distancia de 1 dentro del kernel. Hecho lo anterior podemos proponer el nuevo aproximador de densidad como: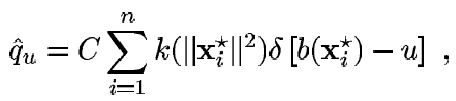
(29)
donde d es la función delta de Kronecker (versión discreta de la función delta) y la constante de normalización
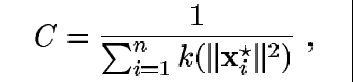(30)
es obtenida si se basa uno en la condición de que 
y que la suma de las funciones delta es igual a 1.
Candidato Objetivo. Vamos a definir{xi*} i=1..n, como todos los píxeles que componen a un posible candidato en el frame actual, el cual esta centrado en 0. Usando el kernel anterior pero con radio h, la probabilidad del color u está dada por:
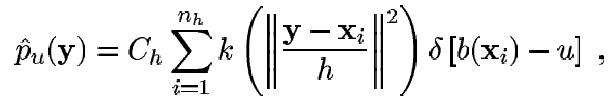(31)
la constante de normalización Ch está dada por:
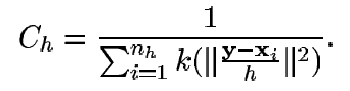(32)
El radio del perfil del kernel determina cuantos píxeles ocupa el candidato objetivo, llamemos a ese numero nh, y nótese que Ch no depende de y, ya que el y puede ser solamente uno de los centros del kernel dado el perfil y el valor de h, por lo tanto Ch puede ser precalculado para varios valores de h.
Minimización de la distancia entre las 2 distribuciones. Una vez definidos los estimadores de distribución, ahora vamos a proceder a minimizar la distancia (28) que es lo mismo que maximizar el coeficiente (27). Una vez que tenemos la posición del centro del objeto modelo y0 en un tiempo t-1, la búsqueda en un tiempo t comienza precisamente alrededor de ese punto, y se espera que el objetivo no se haya movido demasiado de el. Para hacer lo anterior se debe de calcular {pu(y0)}u=1..m y usando la Serie de Taylor para aproximar en un punto y cercano a y0 podemos desarrollar:
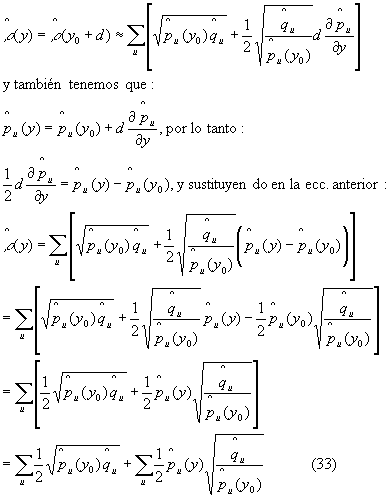
Ahora introduciendo (31) en (33) tenemos
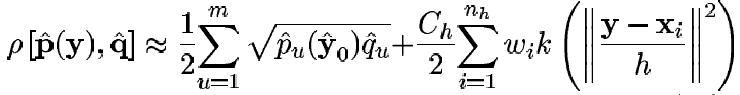(34)
donde
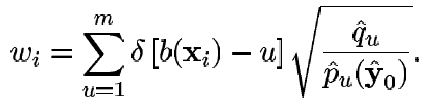(35)
Vamos entonces a maximizar solo el segundo término de (34), ya que el primer término es independiente de y y de esta manera se está minimizando la distancia entre las distribuciones. Aquí es donde entra el método Mean-Shift ya que es una manera iterativa muy eficiente de maximizar este segundo término con el perfil de kernel k y pesado por un peso wi, siendo el siguiente algoritmo implementado para maximizar el coeficiente de Battacharyya.
Encontrar los pesos wi de acuerdo a (35)
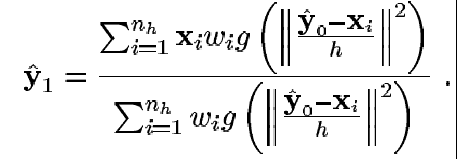(36)
Actualizar {pu(y1)}u=1..m y evaluar
reducir 
e) Si 
parar
de lo contrario hacer 
e ir al paso 5.
Dado que el paso c) no necesariamente incrementa el valor de 
, se hace la prueba del paso d) que valida la nueva posición del objetivo, sin embargo la experimentación indica que solo el 0.1% de los pasos de maximización utilizaron esta protección. El umbral de terminación e del paso e) puede ser calculado para que el proceso finalize cuando y1 y y0 se encuentran en el mismo píxel, con lo cual podemos ver que el método no necesita ser parametrizado adicionalmente.
Adaptación en la escala. Para hacer el escalamiento (recordar que las distribuciones son insensibles a escalas) simplemente se modifica el radio h del perfil del kernel usado en el candidato objetivo. Se han utilizado cambios de +- 10%, dejando al algoritmo de tracking que converja y escogiendo el radio que minimiza la distancia d propuesta. Para un cálculo adecuado del nuevo radio se usa un filtro IIR (Infinite Impulse Response Filter) el cual utiliza una medición actual y el radio anterior. Los IIR tienen mejor respuesta en tiempo real que los FIR y se usan por sus características de predicción adaptativa, una desventaja es que para poder localizar los parámetros deben de ser encontrados los parámetros óptimos del filtro y esto es en si un problema de optimización.
Resultados de Tracking. Las pruebas se hicieron haciendo tracking de una región elipsoide (hx,hy)= (71,53), marcando un jugador de fútbol americano. Para el calculo del histograma se usó el perfil de Epanechnikov y para las iteraciones de Mean-shift se usó el perfil uniforme, lo anterior para que el cálculo del histograma sea rápido y que en las búsquedas de Mean-Shift haya una condición de paro establecida. El histograma del objetivo fue de 32x32x32 barras. El algoritmo (que fué implementado en Java) tiene un desempeño muy adecuado a 30 frames por segundo en una PC de 600 Mhz. Los resultados se presentan en la figura 8, en donde se puede apreciar la robustez a oclusiones parciales, distractores (objetos con características parecidas) y movimientos de la cámara. Se puede observar como el emborronamiento del objeto en algunos frames no afecta el desempeño del tracker.
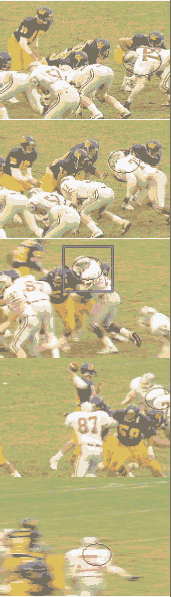
Figura 8.- Frames 30,75,105,140 y 150 del traking del jugador # 75 en una secuencia de video de 154 frames (352 x 240).
La figura 9 muestra el no. de iteraciones de Mean-Shift en cada frame, en el se puede apreciar que el promedio es 4.19.
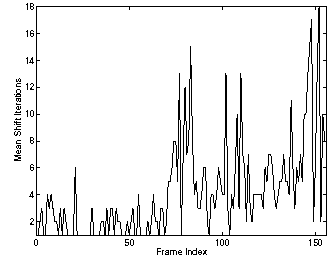
Figura 9.- No. de iteraciones de Mean-Shift por frame.
El autor del trabajo muestra también como el algoritmo es robusto a escalamientos en un video en el cual se hace tracking de una persona en el metro subterráneo, la persona se acerca y se aleja de la cámara cambiando el no. de píxeles que se corresponden al patrón del modelo y el desempeño no se ve afectado. En la figura 10 se muestra el desempeño de la distancia entre los puntos y encontrados como óptimos y el modelo a lo largo de los frames, cuando la distancia es cero tenemos un apareamiento perfecto. Se pude observar los picos debidos a oclusiones parciales y el ultimo pico debido a que la persona desaparece de la escena.
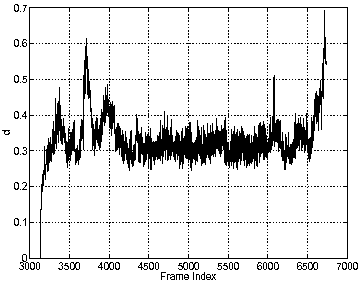
Figura 10.- Valores mínimos de la distancia d detectada a lo largo de los 2 minutos de la secuencia llamada subway2.
Optimización utilizando un filtro de Kalman.
En el análisis anterior se asumió que la posición en donde se localiza el objeto de frame a frame no cambia drásticamente, es por ello que para el mismo pudimos utilizar la expansión a series de Taylor. Pues bien, para lograr un desempeño mas robusto a cambios bruscos, así como reducir el numero de iteraciones de Mean-Shift, los autores utilizaron dos filtros de Kalman, uno para la dirección x y otro para la dirección y del movimiento del objetivo. Para modelar el movimiento se ha presupuesto que tiene una velocidad de cambio leve con ruido blanco de baja varianza (0.01) que afecta la aceleración, además el otro parámetro que se utiliza para que el filtro de Kalman pueda trabajar es la incertidumbre de la localización. La incertidumbre de la localización del objetivo es determinada por el ruido en la imagen, la similitud entre los colores del objetivo y el fondo, los objetos que lo ocultan, y el porcentaje que es ocultado. Como estos mismos factores afectan el valor máximo del Coeficiente de Battacharyya y la curvatura alrededor de este máximo, se puede establecer una relación entre estas dos características (las cuales pueden ser evaluadas en tiempo real) y la incertidumbre de la localización del objetivo.
El modelo utilizando el filtro de Kalman se puede resumir en la Figura 11.
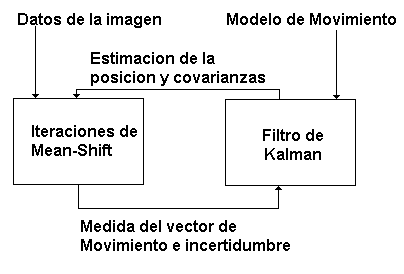
Figura 11.- Diagrama a Bloques de los módulos cuando se utiliza un filtro de Kalman.
A continuación se presenta una muy breve descripción de como trabaja un filtro de Kalman.
El filtro de Kalman ataca el problema esencial de estimar el estado x
Î Rn de un proceso discreto controlado en tiempo, el cual es gobernado por una ecuación lineal estocástica
(37)
con una medición z Î Rm como
(38)
las variables aleatorias wk y vk representan el ruido del proceso y de la medición respectivamente, las cuales se asumen como ruido blanco con matrices de covarianza Q y R respectivamente, las cuales son bandadas.
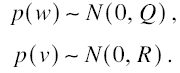(39)
La matriz A de nxn relaciona el estado en el paso anterior k-1 con el estado actual en el paso actual. La matriz B de nxl es la entrada de control u Î Rn (opcional) al estado x. La matriz H de mxn en la ecuación de medida relaciona el estado x a la medida zk.
Definiciones:
Estimación a priori del estado en el paso k dado conocimiento a priori del proceso en el paso k.
Estimación del estado a posteriori en el paso k dada la medida zk.
Estimación de Error a priori.
Estimación de Error a posteriori.
Covarianza del estimador de error a priori.
Covarianza del estimador de error a posteriori.
Pues bien, el objetivo es encontrar una ecuación que calcule un estimador de estado a posteriori xk como una combinación lineal de un estimador de estado a priori 
y una diferencia entre la actual medición zk y la medición predicha 
la cual es pesada por una matriz K de nxm.
(40)
La matriz K (conocida como ganancia Kalman) es escogida de tal forma que minimice la covarianza del error a posteriori Pk. Haciendo sustituciones se puede llegar a la forma
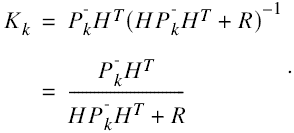(41)
El filtro de Kalman estima el proceso usando una forma de control basado en retroalimentación: el filtro estima el estado del proceso y entonces obtiene retroalimentacion en forma de mediciones. Las ecuaciones del filtro de Kalman se separan en 2 grupos: Ecuaciones de Actualizacion del tiempo y Ecuaciones de actualizacion de la medicion. Las primeras son las encargadas de proyectar hacia adelante (en el tiempo) el estimador de estado actual y el estimador de Covarianza para obtener estimadores a priori para el siguiente paso en el tiempo, mientras que las segundas son las responsables de retroalimentar, es decir, incorporar una nueva medición en el estimador a priori para obtener un estimador a posteriori mejorado.
La ecuaciones de actualización en el tiempo se pueden ver como ecuaciones predictoras mientras que las ecuaciones de actualización de medida se pueden ver como ecuaciones correctoras. Usando las ecuaciones anteriores se puede realizar un diagrama de la operación del filtro de Kalman, el cual se muestra en la Figura 12.
Figura 12.- Diagrama a bloques de un filtro de Kalman.
Interfase al filtro de Kalman
El filtro de Kalman recibe entonces el vector que entregan las iteraciones de Mean-Shift y una medida de incertidumbre. Por ultimo, la incertidumbre del modelo, la cual es obtenida mediante la evaluación del máximo del coeficiente de Battacharyya y la curvatura en una vecindad, es alimentada al filtro de Kalman mediante la modificación de la matriz de covarianzas R, ya que si esta matriz tiene valores pequeños, el filtro de Kalman le dará gran validez a la medición obtenida y por el contrario si tiene valores grandes el filtro es mas lento para responder a las mismas.
REFERENCIAS