En 1996, Mark Kac [6]
propuso la siguiente pregunta: se puede oir la forma de un tambor? O sea,
una región ![]() del plano es determinada por el espectro del Laplaciano en
del plano es determinada por el espectro del Laplaciano en ![]() ? La respuesta es NO, y las siguientes dos regiones
dan un contraejemplo:
? La respuesta es NO, y las siguientes dos regiones
dan un contraejemplo:

Antes que todo, observemos que las regiones no son isométricas,
lo que en el plano significa que no podemos sobreponer una a la otra. Resta
ver que son isoespectrales. La demostración de que esas dos regiones
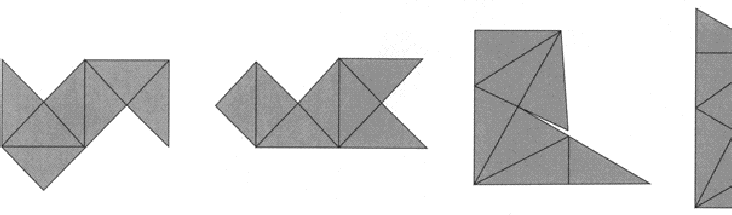
son isoespectrales es bien simple e ingeniosa. Se divide la región ![]() en 7 triángulos isósceles denominados A,
en 7 triángulos isósceles denominados A, ![]() , G, como en la figura. Considere
, G, como en la figura. Considere ![]() una auto-función de
una auto-función de ![]() en
en ![]() , esto es,
, esto es, ![]() . Es claro que f restricta a alguno de los triángulos es
una auto-función sobre ese triángulo. Es más, si tomamos
f sobre dos triángulos cualesquiera, por ejemplo F
y A, y definimos g sobre un triângulo congruente T
como siendo la suma F+A de los valores de f sobre
F con los valores de f sobre A,
. Es claro que f restricta a alguno de los triángulos es
una auto-función sobre ese triángulo. Es más, si tomamos
f sobre dos triángulos cualesquiera, por ejemplo F
y A, y definimos g sobre un triângulo congruente T
como siendo la suma F+A de los valores de f sobre
F con los valores de f sobre A,![]() g será una auto-función asociada al auto-valor
g será una auto-función asociada al auto-valor ![]() :
:
![]()
Lo mismo, naturalmente, valdrá para sumas y diferencias arbitrárias
entre los ``pedazos''. Así, la función g definida
en ![]() como muestra la figura:
como muestra la figura:
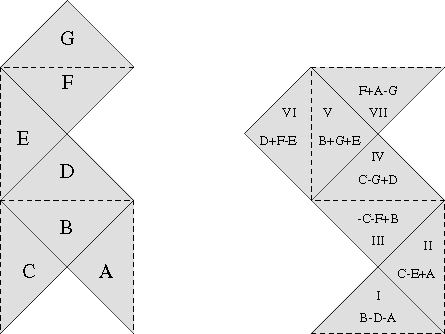
será una auto-función asociada a ![]() en cada triángulo. Resta verificar que g ``se pega''
en cada triángulo. Resta verificar que g ``se pega'' ![]() entre un triángulo y otro, y que
entre un triángulo y otro, y que ![]() .
.
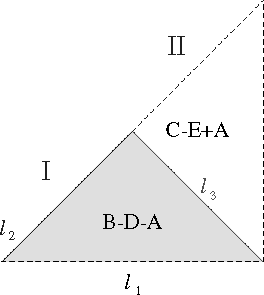
Vamos a mostrar explícitamente la verificación para el paso entre los triángulos I y II:
Cómo se encontraron estos tambores?
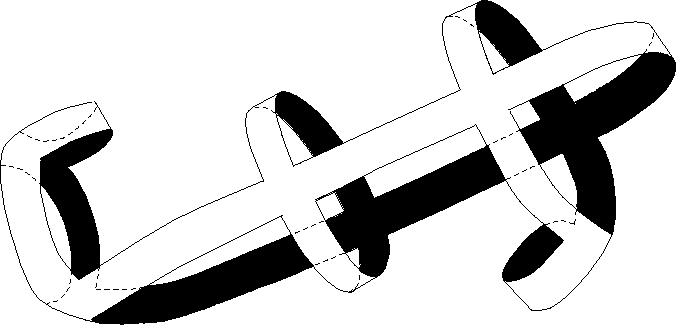
En [1], Buser contruye dos superficies isoespectrales no planas, representadas en la figura:

A partir de ellas, esencialmente cortándolas al medio y ``aplastándolas'' en el plano, C. Gordon , D. Webb y S. Wolpert [5] contruyeron la primera versión de tambores diferentes e isoespectrales:
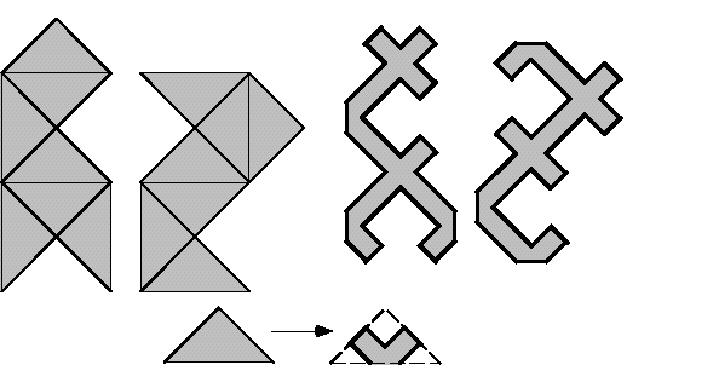
La demostración de que esas regiones montadas con media-cruzes son isoespectrales es esencialmente la misma que dimos para las regiones montadas contriángulos (el lector puede verificar que ella se aplica). En verdad esta demostración fue hecha originalmente para las versiones media-cruz de los tambores [8]. Observándose que la prueba no depende del formato exacto de la pieza fundamental que genera las regiones, sino principalmente de la forma como se pegan esatas piezas, se puede construir diversos tambores diferentes simplemente usando piezas fundamentales diferentes.
Lo que nos resta hacer es contruir las variedades de Buser. En [7], Sunada demuestra el siguiente teorema
Teorema.[Sunada]
Sea G un grupo finito actuando libremenet e isométricamente
en una variedad riemanniana compacta M. Suponga que ![]() y
y ![]() sean subgrupos de G tales que cada clase de conjugación [g] en G
intersepte
sean subgrupos de G tales que cada clase de conjugación [g] en G
intersepte ![]() y
y ![]() en el mismo número de elementos, i.e.
en el mismo número de elementos, i.e.
![]()
Entonces ![]() y
y ![]() son isoespectrales.
son isoespectrales.
Buser usa ese teorema para el grupo G=SL(3,2) de las matrices ![]() invertíbles con coeficientes en
invertíbles con coeficientes en ![]() . Los subgrupos son:
. Los subgrupos son:

Antes de todod, verifiquemos que esos subgrupos satisfacen las hipótesis del teroema de Sunada.
Podemos pensar en ![]() como el subgrupo de las matrices que preservan
como el subgrupo de las matrices que preservan ![]() . Así,
. Así, ![]() síy sólo si
síy sólo si ![]() tiene a
tiene a ![]() como auto-vector (auto-valor 1). Esto es, síy solamente si
como auto-vector (auto-valor 1). Esto es, síy solamente si ![]() es auto-vector de g. Como
es auto-vector de g. Como ![]() puede asumir cualquier valor en G,
puede asumir cualquier valor en G, ![]() depende solamente de cuantos autovectores tiene g. Así, [g]
y
depende solamente de cuantos autovectores tiene g. Así, [g]
y ![]() interseptan
interseptan ![]() en el mismo número de elementos. pero es fácil ver que el
automorfismo
en el mismo número de elementos. pero es fácil ver que el
automorfismo ![]() lleva
lleva ![]() exactamente en
exactamente en ![]() , portanto
, portanto ![]() intersepta
intersepta ![]() tantas veces cuanto [g] intersepta
tantas veces cuanto [g] intersepta ![]() . Como
. Como ![]() es un grupo,
es un grupo,
![]()
Ahora note que
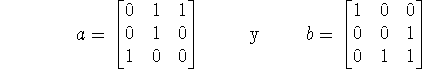
generan G.
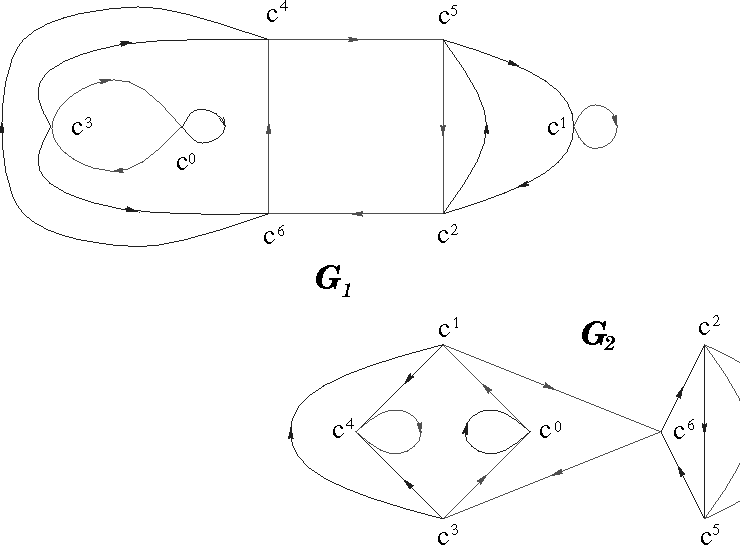
Vamos a considerar ![]() , el gráfico de Cayley de G, con generadores a, b.
El grupo G actúa en
, el gráfico de Cayley de G, con generadores a, b.
El grupo G actúa en ![]() de forma natural y vamos a considerar los gráficos
de forma natural y vamos a considerar los gráficos ![]() y
y ![]() . Para entender esos gráficos, vamos a estudiar las clases laterales
de
. Para entender esos gráficos, vamos a estudiar las clases laterales
de ![]() y
y ![]() .
.
Considere o conmutador
Ese elemento tiene orden 7 y ![]() si y sólo si
si y sólo si ![]() (mod 7), por tanto las clases laterales
(mod 7), por tanto las clases laterales ![]() son disjuntas para diferentes (mod 7) valores de k (ver apéndice).
Además, los
son disjuntas para diferentes (mod 7) valores de k (ver apéndice).
Además, los ![]() cubren todo G, por tanto para cada k existirá un único
exponente
cubren todo G, por tanto para cada k existirá un único
exponente ![]() tal que
tal que ![]() (ver apéndice). Análogamente, hay un único
(ver apéndice). Análogamente, hay un único ![]() tal que
tal que ![]() . Esos exponentes nos dicenque, en el gráfico
. Esos exponentes nos dicenque, en el gráfico ![]() , el elemento representado por
, el elemento representado por ![]() es llevado a
es llevado a ![]() cuando es multiplicado por a. Cuando es multiplicado por b,
va a
cuando es multiplicado por a. Cuando es multiplicado por b,
va a ![]() . Así, basta conocer
. Así, basta conocer ![]() y
y ![]() para construir los gráficos
para construir los gráficos ![]() . Damos abajo tabla que define
. Damos abajo tabla que define ![]() y
y ![]() (ver apéndice):
(ver apéndice):
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 1 | 6 | 0 | 5 | 2 | 4 | |
| 0 | 2 | 5 | 6 | 3 | 1 | 4 | |
| 1 | 6 | 5 | 0 | 4 | 2 | 3 | |
| 0 | 4 | 5 | 1 | 3 | 6 | 2 |
A partir de las tablas es fácil construir los gráficos.
Por ejemplo, ![]() tiene 7 elementos, representados por
tiene 7 elementos, representados por ![]() y que están denominados por k. Las flechas contínuas
representan el producto por a y las líneas punteadas, el
producto por b. La tabla dice que
y que están denominados por k. Las flechas contínuas
representan el producto por a y las líneas punteadas, el
producto por b. La tabla dice que ![]() . Así, el producto de a por el vértice 5 debe dar
el vértice 2.
. Así, el producto de a por el vértice 5 debe dar
el vértice 2.
Así, tenemos bien estudiado el grupo G, sus subgrupos ![]() y
y ![]() y los cocientes
y los cocientes ![]() ,
, ![]() . Pero cuál será la variedade M que necesitamos para
aplicar el teorema de Sunada? Vamos a asociar a cada vértice g
del gráfico de Cayley
. Pero cuál será la variedade M que necesitamos para
aplicar el teorema de Sunada? Vamos a asociar a cada vértice g
del gráfico de Cayley ![]() de G, una cruz con los segmentos del borde denominados como en la
figura.
de G, una cruz con los segmentos del borde denominados como en la
figura.
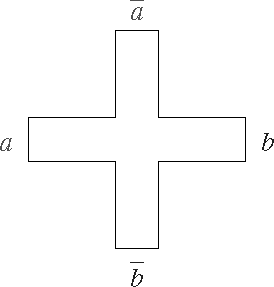
FIGURA 8.
Después identificarempos dos puntas de dos cruces en el siguiente
caso: si ![]() , identificamos el borde a de la cruz asociada a
, identificamos el borde a de la cruz asociada a ![]() con el borde
con el borde ![]() de la cruz asociada a
de la cruz asociada a ![]() . Análogamente, para
. Análogamente, para ![]() , identifícase b de la primera cruz con
, identifícase b de la primera cruz con ![]() de la segunda.
de la segunda.
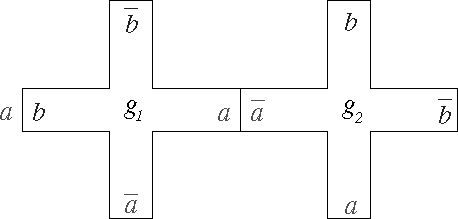
Es claro que cada borde a, ![]() , b ó
, b ó ![]() de cada cruz estará identificada algún otro borde. Sea M
la variedad resultante de estas identificaciones. Cada
de cada cruz estará identificada algún otro borde. Sea M
la variedad resultante de estas identificaciones. Cada ![]() lleva la cruz
lleva la cruz ![]() en la cruz
en la cruz ![]() isométricamente de forma natural. Así, G actúa
libremente e isométricamente en M y por tanto, por el teorema
de Sunada,
isométricamente de forma natural. Así, G actúa
libremente e isométricamente en M y por tanto, por el teorema
de Sunada, ![]() y
y ![]() son isoespectrales. Las variedades
son isoespectrales. Las variedades ![]() y
y ![]() pueden ser visualizadas a partir de los gráficos
pueden ser visualizadas a partir de los gráficos ![]() y
y ![]() . Basta hacer el mismo collage de cruces para
. Basta hacer el mismo collage de cruces para ![]() y tendremos variedades cociente isoespectrales y claramente no isométricas.
Esas variedades, entretanto, no pueden ser colocadas isométricamente
en el plano, no son ``tambores''. Si pegamos la ``mitad'' de cada una de
ellas, cortando a lo largo de las líneas indicadas en la figura:
y tendremos variedades cociente isoespectrales y claramente no isométricas.
Esas variedades, entretanto, no pueden ser colocadas isométricamente
en el plano, no son ``tambores''. Si pegamos la ``mitad'' de cada una de
ellas, cortando a lo largo de las líneas indicadas en la figura:
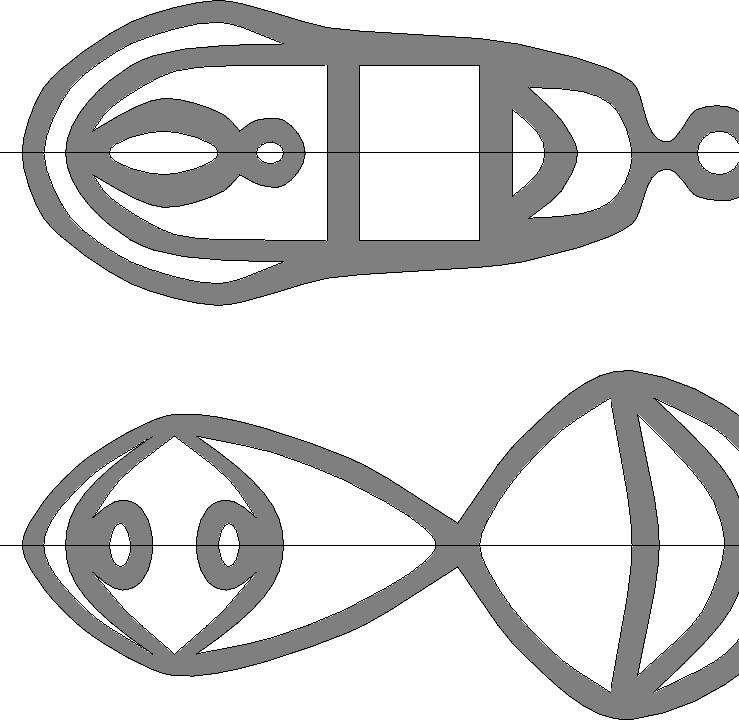
tendremos entonces dos figuras formadas por 7 media-cruces, que pueden se incrustadas isométricamente en el plano dando ``tambores'' satisfactorios.
Como ya dijimos, esos dos tambores son, esencialmente, los mismos que presentamos en el inicio del texto.
Apéndice.
Demostraremos aquíalgunas propidades de SL(3,2) que usamos
para la construcción de los gráficos ![]() y
y ![]() . Primeramente, verifiquemos que, si
. Primeramente, verifiquemos que, si ![]() para
para ![]() , entonces
, entonces ![]() , donde
, donde ![]() y portanto
y portanto ![]() (mod 7). Así, las clases laterales de
(mod 7). Así, las clases laterales de ![]() son disjuntas.
son disjuntas.
Seguimos esrcibiendo explícitamente algunos elementos de G:
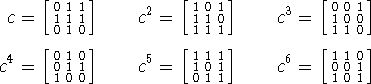
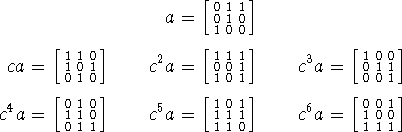
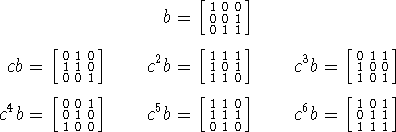
Verificamos por las lista que la única potencia ![]() del conmutador
del conmutador ![]() que pertenece a
que pertenece a ![]() ó
ó ![]() es
es ![]() .
.
También es fácil ver que ![]() tiene 24 elementos. Existen 8 vectores en
tiene 24 elementos. Existen 8 vectores en ![]() . Podemos llenar las dos columnas libres de un elemento de
. Podemos llenar las dos columnas libres de un elemento de ![]() de
de ![]() formas diferentes: en la primera columna vacante podemos colocar cualquiera
de los 6 vectores diferentes del nulo y de
formas diferentes: en la primera columna vacante podemos colocar cualquiera
de los 6 vectores diferentes del nulo y de ![]() , la primera columna. En la tercera, podemos colocar culaquier vector que
no sea uno de los dos ya excluídos, o el escogido para ocupar la
segunda columna, o la suma de la primera columna con la segunda, esto nos
da 4 opciones para llenar la última columna. Como
, la primera columna. En la tercera, podemos colocar culaquier vector que
no sea uno de los dos ya excluídos, o el escogido para ocupar la
segunda columna, o la suma de la primera columna con la segunda, esto nos
da 4 opciones para llenar la última columna. Como ![]() y
y ![]() son isomorfos, ambos tienen 24 elementos.
son isomorfos, ambos tienen 24 elementos.
Ya vimos que las clases laterales ![]() son todas distintas. Por tanto la unión de ellas totaliza los
son todas distintas. Por tanto la unión de ellas totaliza los ![]() elementos de G, esto es, cubren todo G. Lo mismo se aplica
a
elementos de G, esto es, cubren todo G. Lo mismo se aplica
a ![]() .
.
Vemos, a seguir, cómo construir la tabla de las funciones ![]() y
y ![]() .
.
Vamos a comenzar construyendo la tabla de ![]() . Vamos a hacerla al contrario: achar qué k debe ser llevado
en un dato
. Vamos a hacerla al contrario: achar qué k debe ser llevado
en un dato ![]() . Necesitamos consultar las listas de
. Necesitamos consultar las listas de ![]() y
y ![]() . Queremos estudiar la relación entre k y n tales
que
. Queremos estudiar la relación entre k y n tales
que ![]() . Note que
. Note que ![]() lleva algún vector
lleva algún vector ![]() en el vector
en el vector ![]() , invariante por los lelementos de
, invariante por los lelementos de ![]() . Es decir, todo elemento de
. Es decir, todo elemento de ![]() llevará x en
llevará x en ![]() . Basta verificar en la lista de los
. Basta verificar en la lista de los ![]() cuál elemento hace esto (es claro que por el estudio que hicimos
de las clases laterales que hay uno y sólo un tal elemento). Asítendremos
cuál elemento hace esto (es claro que por el estudio que hicimos
de las clases laterales que hay uno y sólo un tal elemento). Asítendremos ![]() .
.
Por ejemplo, tomando n=2, buscaremos k tal que ![]() . Hallando la solución x de
. Hallando la solución x de ![]() , tenemos:
, tenemos:
![]()
Verificamos en la lista que el elemento ![]() que lleva x en
que lleva x en ![]() es ca:
es ca:
![]()
Abajo representamos la lista de todos los ![]() y los respectivos
y los respectivos ![]() . Notemos que lo mismo puede ser aplicado a los
. Notemos que lo mismo puede ser aplicado a los ![]() .
.
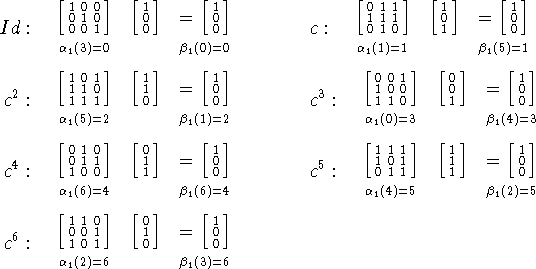
Hallar ![]() y
y ![]() es más fácil. El subgrupo
es más fácil. El subgrupo ![]() está formado por las matrices que preservan el plano
está formado por las matrices que preservan el plano ![]() . De forma análoga a lo que hicimos arriba para
. De forma análoga a lo que hicimos arriba para ![]() , podemos estudiar
, podemos estudiar ![]() . Así, debemos preguntarnos qué espacio es llevado a
. Así, debemos preguntarnos qué espacio es llevado a ![]() por
por ![]() . Esto es, cuáles on los vectores cuya imágen por
. Esto es, cuáles on los vectores cuya imágen por ![]() tiene primera coordenada 0. Ese espacio deberá ser llevado por
tiene primera coordenada 0. Ese espacio deberá ser llevado por ![]() en símismo, o sea, la imágen deberá tener primera
coordenada 0. Es fácil ver que para que pase eso es necesario que
las primeras líneas de
en símismo, o sea, la imágen deberá tener primera
coordenada 0. Es fácil ver que para que pase eso es necesario que
las primeras líneas de ![]() y
y ![]() sean iguales. Por ejemplo, tomemos n=2:
sean iguales. Por ejemplo, tomemos n=2:

Esto es, los vectores con primera y última coordenadas iguales
son llevados en el subespacio invariante por ![]() , por tanto
, por tanto ![]() debe llevarlos en los vectores con primera coordenada 0. Es claro que la
primera línea de
debe llevarlos en los vectores con primera coordenada 0. Es claro que la
primera línea de ![]() debe ser
debe ser ![]() , la primera línea de
, la primera línea de ![]() . Como el único
. Como el único ![]() con esta línea es
con esta línea es ![]() , tendremos que
, tendremos que ![]() .
.
Haciendo lo mismo con todos los n:
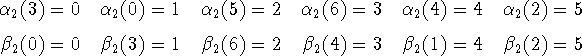
Esto completa la construcción de la tabla de productos en ![]() .
.