Veamos que si tenemos un nudo en ² entonces k₀(S¹ ) separa el plano en dos pedazos, uno que llamaremos el interior, que es el que encierra la curva y otro que queda fuera de esta.

TEOREMA DE LA CURVA DE JORDAN: Si k₀:S¹®Â² es un nudo, entonces ²-k₀(S¹) tiene exactamente dos componentes.

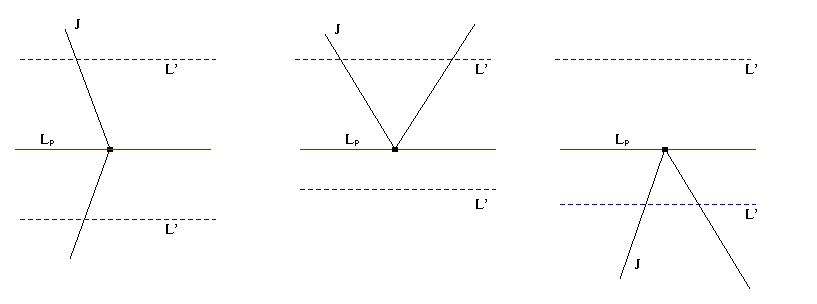
DEMOSTRACION: Llamemos J=k₀(S¹). Entonces, J está formado por un número finito de rectas (esto por la def. de nudo), como hay una infinidad de direcciones en el plano, podemos escoger una recta L Ì Â² que no sea paralela a ninguno de los segmentos de J. Tomamos a L como el eje x. Tenemos entonces que ningún segmento de recta es horizontal. Definimos una función f:²-J®{0,1}. Sea, pues, p Π²-J; sea L_p la recta horizontal que pasa por p.

1er. caso. Si L_p no pasa por ningún vértice de J, entonces definimos:
f(p):=número de puntos de L_pÇJ que están a la izquierda de p módulo 2.

2do. caso. Si L_p pasa por un vértice de J, tomamos L¢ paralela a L_p que esté muy cerquita de L_p y tal que L¢ no pase por ningún vértice de J. Definimos en este caso:
f(p):=número de puntos de L¢ÇJ que están a la izquierda de p módulo 2.
Nótese que si tiene sentido ëstar a la izquierda de p", pues por el punto p pasa una recta vertical para las que tiene sentido hablar de su "derecha" o ïzquierda". Este número, módulo 2, es igual para todas las rectas L¢ que estén muy cerca de L_p. Por tanto f está bien definida.

Además, por la definición de f si dos puntos p,q Π²-J están muy cerquita, se cumple que f(p)=f(q), es decir, f es una función continua. (Pensando en la definición de continuidad).
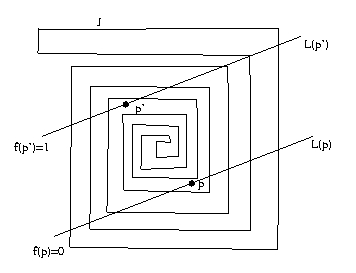
También es fácil ver que f es una función suprayectiva ya que: si tomamos una recta horizontal M que no interseca J (esto es posible porque J está acotado en ²), entonces f(p)=0  "p Î M. Si M interseca a J y no pasa por ningún vértice de J en tonces por estar J acotado, se tiene que MÇJ tiene un primer punto p^* que está mas a la izquierda que todos los demás puntos de esta intersección. Tomemos entonces un punto p Π²-J que esté en M un poquito a la derecha de p^*; por tanto f(p)=1. Por tanto f es suprayectiva.

Tenemos entonces una función f:²-J®{0,1} continua y suprayectiva, esto es posible sólo si ²-J tiene al menos dos componentes.

Demostremos ahora que ²-J tiene a lo más dos componentes. Construimos una vecindad de J con pedacitos convexos de ². Sobre cada vértice de J colocamos un disco no muy grande (de tal manera que sólo intersecte a sus dos aristas adyacentes en radios del disco) y sobre cada arista de J colocamos un rectángulo flaquísimo (tan flaco que cubra a la arista pero con la condición de que intersecte sólo a dos de sus aristas adyacentes y que dicha intersección esté dentro de los discos que cubren a sus vértices).

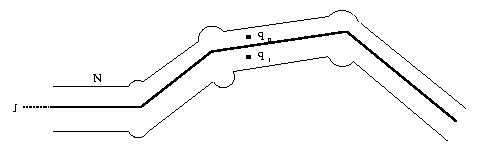
Llamamos N a esta vecindad de J. En uno de los rectángulos de N, escogemos dos puntos q₁,q₂ Î N-J que esten en lados opuestos de J. Si p Î N-J, es claro que podemos conectar a p con q₁ o con q₂, mediante una trayectoria poligonal contenida en N-J; tenemos así un segmento de recta l Ì Â²-J que conecta a q con algún punto p Î N-J. Como podemos conectar a p con q₁ o con q₂ mediante una poligonal en N-J, resulta que podemos conectar a q con q₁ o bien con q₂, mediante una poligonal contenida en ²-J. Concluimos que ²-J tiene cuando mucho dos componentes.
Por lo tanto ²-J tiene exactamente dos componentes.

Regresar a Introducción

Regresar

Página principal