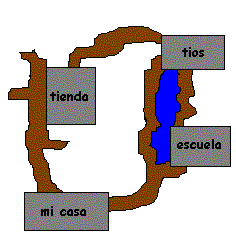
Figura 1.1
Mapa de un camino cotidiano (calles y sitios)
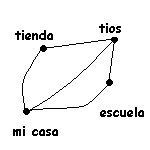
Figura 1.2
Representación en términos de grafos de calles y sitios.
1 Introducción a los grafos
1.1 Grafos
1.2 Representación computacional
1.3 Familia de grafos
1.4 Problemas iniciales
1.4.1 Caminos
1.4.2 Arqueología OMIca
1.4.3 Yacimientos
1.4.4 Callejones
Hoy en día, la aplicación de la computación es requerida en la mayoría de los campos científicos y la teoría de grafos no es la excepción. Por ello, también estableceremos las nociones básicas de su representación computacional y mostraremos algunos algoritmos y problemas clásicos en grafos.
Si vemos el mapa de una ciudad, sus calles y puntos sobresalientes puede ser representados a través de líneas (las calles) y puntos (lugares relevantes). Por ejemplo:
 |
 |
Figura 1.1 |
Figura 1.2 |
Existen muchas aplicaciones de grafos en problemas reales. De hecho, basta con que un conjunto de objetos tengan una relación por parejas para formar grafos. Ya que cada objeto se puede representar como un punto (vértice) y cada relación entre dos objetos como una línea (arista). De este modo, podemos pensar en problemas de relaciones entre dependecias. Cada departamento esta representado como un nodo mientras que una línea (es decir, una arista) representaría si existe alguna relación o dependencia de un departamento a otro. Más adelante mostraremos diversos ejemplo donde un problema puede ser representado como un grafo.
El anterior esquema muestra los caminos disponibles de un lugar a otro. De este modo, podemos simplificar el dibujo de la figura 1.1 como en la figura 1.2 éste esquema más llano será llamado grafo. Geométricamente hablando, un grafo es un conjunto V de puntos en el espacio, llamados nodos o vértices, interconectados por medio de un conjunto A de líneas, llamadas aristas. Denotaremos G(V,A) al grafo cuyo conjunto de vértices es V y cuyo conjunto de aristas es A. Desde ahora supondremos que el número (cardinalidad) de vértices y aristas es finita (es decir, que no hay infinitas aristas o vértices). Es posible formalizar la definición anterior como sigue:
Definición 1.1.1: Un grafo G(V,A), es una estructura matemática consistente en dos conjuntos V y A. Los elementos de V son llamados vértices (o nodos), y los elementos de A son llamados aristas. Cada arista tiene asociado un conjunto de uno o dos vértices, los cuales llamaremos extremos.
En nuestro ejemplo inicial, los vértices son cuatro: "mi casa", "tios", "tienda", "escuela". Además tenemos 5 aristas que podemos identificar como los caminos:
Antes de seguir, aclaremos que la cardinalidad de un conjunto (en palabras sencillas) es el número de elementos que tiene el conjunto en cuestión. Para nuestro mapa, hemos creado un grafo cuya cardinalidad (número) de su conjunto de vértices (los puntos relevantes) es 4 mientras que la cardinalidad del conjunto de aristas (los caminos entre los puntos relevantes) es de 5. Por otro lado, para poder indicar de qué aristas hablamos, basta con decir cuales son los extremos que tiene dicha aristas. En ocasiones, dos o más aristas tienen el mismo par de vértices por extremo. Lo cual puede representar dos o más caminos diferentes en un mapa o diferente tipo de relaciones entre individuos. Aunque en la mayoria de los problemas olímpicos no hay grafos con aristas dobles, es necesario tener una forma de identificar de cual arista hablamos si se presenta el caso. Por tanto, hagamos la siguiente notación para poder referirnos a las aristas de manera formal.
Notación 1.1.1: La arista del grafo G(V,A) que interconecta los vértices i y j será denotada Ak(G,i,j). Donde k es un indice, único de la arista, en el caso existir dos o más aristas con el mismo par de vértices. Cuando no exista ambigüedad sobre el grafo abreviaremos como Ak(i,j). Y en caso de sólo existir una arista, por cada par de vértices, omitiremos el indice superior denotando simplemente como A(i,j). Los vértices i y j también los podemos nombrar como los extremos de A(i , j). Si aij = A(i , j) denotamos como: ext(aij ) ={ i , j }. Es decir, si u es una arista, ext(u) denota el conjunto que contiene a los vértices que son los extremos de la arista u.
Notación 1.1.2: Sea G(V,A) un grafo con número finito de vértices y aristas; denotaremos |V| la cardinalidad de V y |A| la cardinalidad de A.
Notemos que la distancia de cada camino es relevante para nuestro objetivo (pues deseamos llegar lo más rápido a la casa de los tios). De este modo, Si el camino casa-tios tiene un largo de 0.8 km, el camino de casa-escuela 0.4 km y el camino de escuela-tios 0.3 km. Entonces es lógico que seleccionemos irnos por la ruta de la escuela (casa-escuela, escuela-tios) recorriendo un total de 0.7 km en lugar de los 0.8 km. Por esta razón, en ocasiones, las aristas tienen asignados valores que representan el costo, distancia o fortaleza en la relación de los vértices que unen. Este tipo de arista se llama ponderada y se dice que el grafo es poderado cuando sus aristas tienen asigandos valores (aristas ponderadas). En este caso el grafo tiene asociado un tercer conjunto W que contiene los valores ponderados asignados a cada esquina.
Notación 1.1.3: El valor ponderado de las aristas del grafo G(V,A) será denotado como W k (G,i,j). Donde k es un indice, único de la arista, en el caso existir dos o más aristas con el mismo par de vértices. Cuando no exista ambigüedad sobre el grafo abreviaremos como W k (i,j). Y en caso de sólo existir una arista, por cada par de vértices, omitiremos el indice superior denotando simplemente como W(i,j). Si u es un arista, entonces W(u) denota el valor ponderado de la arista u.
El valor ponderado de las aristas por lo común es un conjunto de valores constantes. Sin embargo, es posible que los valores ponderados cambien conforme alguna función dada. En general, nosotros trabajaremos con grafos con valores ponderados constantes pero no olvidemos que estos valores son más que valores constantes. Un ejemplo sencillo: un camión que recolecta basura a lo largo de la calle; entre más basura recoge, más es el costo de viajer entre calle y calle (debido a que tiene más carga que transportar). Por tanto, el valor ponderado de una calle depende de qué tan cargado pase el camión y no es un valor constante.
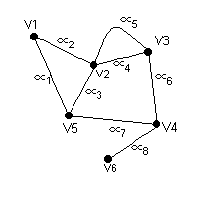
Figura 1.1.1
Grafo G(V,A) con 6 vértices y 8 aristas con sus respectivos
valores ponderados del conjunto W
En la anterior figura tenemos un grafo G(V,A), con el conjunto de
vértices:
V = { v1,
v2 , v3,
v4, v5,
v6 }
el conjunto de valores ponderados W:
W = { α1, α2,
α3, α4,
α5, α6,
α7, α8}.
y el conjunto de aristas como:
A = {A(1,2), A(1,5),
A1(2,3),
A2(2,3),
A(3,4), A(4,5), A(4,6)}.
Es de manera natural referirse como vértices adyacentes, a dos vértices que están relacionados (conectados) por una arista. Análogamente aristas adyacentes son dos aristas aij = A(vi,vj) y akl = A(vk,vl), que tienen un extremo en común. Es decir, vi = vk ó vi= vl ó vj = vk ó vj = vl.
En un mapa, los caminos no siempre se consideran para ambas direcciones, ya que podemos encontrar calles donde el flujo es sólo en un sentido. Por lo tanto, requerimos que un grafo tenga aristas cuya dirección de flujo tenga un solo sentido. Cuando una arista no tiene sentido, se llama arista bidireccionada. De igual modo, cuando las aristas tienen asignado un sentido, se llaman aristas direccionadas. Normalmente, al arista A(i , j) se considera igual a la arista A(j , i) cuando se trata de aristas bidireccionadas pero se consideran diferentes cuando son aristas direccionadas. Formalizando las definiciones:
Definición 1.1.2: Una arista direccionada es una arista en el cual uno de sus extremos es llamado cabeza y el otro es llamado cola. Por tanto, la arista cuya cabeza es i y cola es j es diferente a las arista cuya cabeza es j y cola i
Ahora que sabemos qué es un grafo. Veremos como podemos expresarlo en términos de programación. Matemáticamente, la representación de un grafo G(V,A) es a través de una matriz M, de n x n con lo cual representamos el valor ponderado de la aristas aij en la entrada (i,j) de la matriz M. Sin embargo, antes de ver grafos ponderados, veamos como representamos grafos cuyas aristas no son poderadas.
Nota: Cuando hablamos de la entrada (i,j) de una matriz M nos referimos al valor, de la matriz, que se encuentra en el renglon i y columna j.
Volviendo por n-esima ocasión a nuestro ejemplo del mapa. Interpretemos nuestro grafo como una matriz de ceros y unos. Donde un cero en la posición (i,j) representa que hay camino del vértice i al vértice j y un uno, que si hay camino. Entonces, nuestra matriz quedaría como en la figura 1.2.1.

Figura 1.2.1. Matriz que representa al grafo de la Figura 1.2.
Como en nuestro ejemplo los caminos son bidireccionados, entonces la matriz es simétrica (Si trazas una línea desde la esquina superior izquierda hasta la esquina inferior derecha, verás la simetría). Es decir, si la entrada (i,j) toma el valor de cero o uno, entonces también la entrada (j,i).
En programación, una matriz se representa como un arreglo bidimensional. Por lo tanto, imaginemos que tenemos un archivo que contiene con las caracteristicas mencionadas en el formato 1.
Formato 1: El archivo input contiene, en su primera línea, un entero 0 < n < 1000 que representa el número de vértices. Seguidamente vienen n líneas con n enteros que representa a la matriz de un grafo. Un uno en el renglón i, columna j, representa que hay arista del vértice i al vértice j y un cero representa que no hay arista.
|
4 0 1 1 1 1 0 0 1 1 0 0 1 1 1 1 0 |
Input 1.2.1. Archivo de ejemplo
El código para leer este formato de grafo quedaría como el siguiente:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
#include "stdio.h"
int main(void)
{
int i,j,n,**matriz;
FILE *input;
// Intentamos abrir el archivo. Terminamos en caso de
// existir algún problema.
if( (input=fopen("input_1_2_1.txt","r+t")) == NULL )
return 0;
// Leemos la cantidad de vértices.
fscanf(input,"%d",&n);
// Creamos los renglones.
matriz = new int*[n];
for(i = 0; i < n; i++)
{
// Creamos las columnas del renglón i y leemos.
matriz[i] = new int[n];
for(j = 0; j < n; j++)
fscanf(input,"%d",&matriz[i][j]);
}
// Cerramos el archivo.
fclose(input);
// Liberamos la memoria dinámica pedida.
for(i = 0; i < n; i++)
delete[] matriz[i];
delete[] matriz;
return 0;
}
|
Código 1.2.1. Creando un arreglo bidimensional para guardar un grafo.
Ahora definamos un tipo de entrada ligeramente diferente a la anterior:
Formato 2: El archivo input contiene, en su primera línea, un entero 0 < n < 1000 que representa el número de vértices. Seguidamente vienen n líneas con n enteros que representa a la matriz de un grafo ponderado. Un valor 0 < x < 1000, mayor a cero, en el renglón i, columna j, representa que hay arista del vértice i al vértice j con un valor ponderado de x. Un cero representa que no hay arista.
|
4 0 3 2 0 1 0 3 1 2 0 0 4 1 3 2 0 |
Input 1.2.2. Archivo de ejemplo
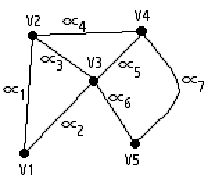 |
 |
| Figura 1.2.2 Grafo G(V,A) |
Figura 1.2.3 Matriz M con los valores ponderados de las aristas del grafo G |
En la figura 1.2.2 mostramos un grafo G(V,A) tal que:
De este modo, la matriz M representa los valores ponderados de cada arista de acuerdo a sus entradas. Es así como podemos determinar el valor de cada arista ponderada en un sistema coordenado, las entradas cuyo valor es cero, se refieren a una arista no existente en G, por lo tanto es necesario suponer (en este caso en particular) que el valor ponderado de las aristas nunca toma el valor de cero. Insistimos que en el caso de un grafo no direccionado, la matriz es simétrica, lo que no necesariamente se cumple en un grafo direccionado.
Es importante hacer notar, que nuestro código 1.2.1 sirve también para grafos direccionados, ya que lee la matriz completa y los valores M[i][j] y M[j][i] pueden ser diferentes sin ningún problema. Más aun, es posible guardar grafos ponderados teniendo la consideración que el valor cero representa que no hay camino en las aristas. De este modo, un grafo, como en la figura 1.2.2, puede ser representado como la matriz de la figura 1.2.3.
Nuestro problema de leer grafos estaría resuelto si siempre tuvieramos entradas como se mostraron en el formato 1 y 2. Sin embargo, en muchos casos no corremos con tal suerte. Otra manera (y quizás la más común) es dar el número de vértices y aristas. Esto tiene mucho sentido, ya que un grafo de muchas veces conocemos como se relacionan los individuos únicamente y no tenemos pregenerada la matriz que requerimos. A continuación establecemos el formato 3 considerando que el grafo no tiene valores ponderados y cuyo ejemplo representa al grafo de la figura 1.2.2.
Formato 3: El archivo input contiene, en su primera línea, dos enteros <0 < n < 1000 y k que representan el numero de vértices y aristas respectivamente. Seguidamente vienen k líneas con 2 enteros cada una y que representan a las k aristas del grafo. Los enteros v y u, de cada línea, representan los extremos de la arista en cuestión. Los vértices son enumerados a partir de cero.
|
5 7 0 1 0 2 1 2 1 3 2 3 2 4 3 4 |
Input 1.2.3. Archivo de ejemplo
El formato 3 sirve tanto para grafos bidireccionados como para grafos direccionados. La única diferencia radica al momento de leer los datos. En el código 1.2.2 mostramos el caso de utilizar un grafo bidireccionado aunque basta con omitir la línea 34 para los casos direccionados.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
#include "stdio.h"
int main(void)
{
int i,j,n,k,u,v,**matriz;
FILE *input;
// Intentamos abrir el archivo. Terminamos en caso de
// existir algún problema.
if( (input=fopen("input_1_2_3.txt","r+t")) == NULL )
return 0;
// Leemos la cantidad de vértices.
fscanf(input,"%d %d",&n,&k);
// Creamos los renglones.
matriz = new int*[n];
for(i = 0; i < n; i++)
{
// Creamos las columnas del renglón i e inicializamos las aristas.
matriz[i] = new int[n];
for(j = 0; j < n; j++)
matriz[i][j]=0;
}
for(i = 0; i < k; i++)
{
// Leemos las k líneas y asignamos el valor de uno a las aristas
// correspondientes en ambas direcciones.
fscanf(input,"%d %d",&u,&v);
// marcamos la arista de u a v
matriz[u][v] = 1;
// En el caso de un grafo direccionado, la siguiente línea se omite
// ya que marca la arista de v a u
matriz[v][u] = 1;
}
// Cerramos el archivo.
fclose(input);
// Liberamos la memoria dinámica pedida.
for(i = 0; i < n; i++)
delete[] matriz[i];
delete[] matriz;
return 0;
}
|
Código 1.2.2. Programa para leer un grafo con el formato 3.
Definición 1.2.1: En la jerga de los matemáticos, un vértice aislado es aquel que no tiene aristas que incidan en él. En otras palabras, el vértice no tiene aristas.
Problema 1.2.1
Con base a la definición de vértice aislado (Definición 1.2.1),
debes escribir un algoritmo que determine cuales vértices se encuentran aislados en un grafo dado.
Input: Formato 3
Output: Una sola línea con la lista de los vértices aislados. La lista debe estar
ordenada de menor a mayor y separados por un espacio.
|
|
Para resolverlo, hagamos una lista de todos los vértices disponibles (n en total). La lista la inicializamos con ceros considerando que un cero equivale a que el vértice es aislado. Acontinuación, leemos las aristas y por cada arista marcamos con el valor de 1, en nuestra lista, a los vértices que forman dicha arista. De este modo, marcaremos con un uno (en la lista) a todos los vértices que son extremos de al menos una arista. Por lo tanto, al final solo imprimimos los vértices que permanecieron con cero en la lista.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
#include "stdio.h"
int main(void)
{
int i,n,k,u,v,*lista;
FILE *input,*output;
// Intentamos abrir el archivo. Terminamos en caso de
// existir algún problema.
if( (input=fopen("input_1_2_4.txt","r+t")) == NULL )
return 0;
// Leemos la cantidad de vértices.
fscanf(input,"%d %d",&n,&k);
// Inicializamos nuestra lista de vértices como aislados.
lista = new int[n];
for(i = 0; i < n; i++)
lista[i] = 0;
for(i = 0; i < k; i++)
{
// Leemos las k líneas y marcamos como vértices no aislados a u y v.
fscanf(input,"%d %d",&u,&v);
// marcamos la arista de u a v
lista[u] = 1;
lista[v] = 1;
}
// Cerramos el archivo.
fclose(input);
// Abrimos en modo de escritura el archivo de salida.
output=fopen("output.txt","w+t");
// búscamos los vértices aislados (marcados como ceros)
for(i = 0; i < n; i++)
{
if( lista[i] == 0 )
fprintf(output,"%d ",i);
}
// Cerramos el archivo de salida.
fclose(output);
// Liberamos la memoria dinámica pedida.
delete[] lista;
return 0;
}
|
Codigo 1.2.3. Solución del problema 1.
En muchos problemas de grafos, es muy importante determinar cual es el número de aristas que inciden en cada vértice. Por ello mismo, existe un termino matemático llamado grado de un vértice que refiere a cuantas aristas tienen por uno de sus extremos a un vértice v Entonces, podemos decir que un vértice de grado cero es un vértice aislado.
Definición 1.2.2: El grado de un vértice es el número de vértices que inciden en él. Lo denotamos como Gr(v) = Número de aristas que inciden en el vértice v.
Problema 1.2.2
Calcula el grado de todos los vértices de un grafo dado.
Input: Formato 3
Output: Una sola línea con los grados de lo vértices. La lista debe tener como
primer número el grado del primer vértice, luego el grado del segundo, y asi sucesivamente.
|
|
Por último, veamos un formato de entrada cuando sólo se conocen las aristas y su valor ponderado. Cabe mencionar, que existen otras maneras para codificar la información de un grafo, pero esas las veremos más adelante.
Formato 4: Considere un grafo ponderado G tal que tiene 0 < n < 1000 vértices y k aristas. El archivo contiene dos enteros en su primera línea, que representan a n y k respectivamente. A continuación, vienen k renglones. Cada renglón consiste en una terna de enteros u, v y c indicando la existencia de la arista del vértice u al vértice v con un valor ponderado de 0 < c < 1000. Los vértices estan enumerados a partir del cero.
|
5 7 0 1 2 0 2 2 1 2 3 1 3 1 2 3 4 2 4 3 3 4 1 |
Input 1.2.4. Archivo de ejemplo
Como ya vimos, los grafos pueden representar diferentes problemas y para cada uno de ellos, el grafo tiene ciertas características. Dependiente de estas propiedades podemos clasificar a los grafos, al igual que hacemos con los triángulos dependiendo de los lados o angulos que tienen, de diversos modos.
Si nosotros tenemos un grafo y es posible dibujar todas sus aristas y vértices sin levantar el lápiz (sin importar si pasamos más de una vez por una línea). Entonces decimos que el grafo es conexo. Por ejemplo, el grafo de la figura 1.3.1 es un grafo conexo, debido a que siempre existe un camino de aristas para poder llegar de un vértice cualquiera a otro vértice del mismo grafo. Esto no quiere decir que tracemos sin remarcar alguna que otra arista. En general, poder trazar una figura sin levantar el lápiz es un problema un poco más complejo que veremos mas adelante.
 |
 |
| Figura 1.3.1 Grafo conexo | Figura 1.3.2 Grafo no conexo |
Antes de poder formalizar nuestra definición de grafo conexo, primero tenemos que ver la definición de un camino en un grafo. Asi pues, un camino en un grafo es una secuencia de aristas de tal forma, que dos aristas consecutivas, en la secuencia, comparten un vértice como extremo. Precisamente se dice camino, porque es posible desplazarte por las aristas como si fueran caminos. Por lo anterior, también es posible ver un camino como una secuencia de vértices de tal modo que; para cada par de vértices consecutivos, siempre existe una arista con dichos vértices por extremos.
Definición 1.3.1: Un camino entre v i y v j en un grafo G(V,A) es una secuencia de vértices v 1 , v 2 ,... v n tal que A(v i , v i + 1 ) es una arista para 1 < i < n, a cada una de estas aristas la llamaremos paso. Si existe un camino entre v i y v j decimos que v i y v j están conectados.
Notemos que de la anterior definición podemos razonar que un camino está formado de aristas y vértices. Por lo tanto, es un grafo. Ahroa que tenemos la noción de un camino, podemos definir a un grafo conexo (aunque ya tenemos la idea intuitiva) y otro termino colado :).
Definición 1.3.2: Un camino cerrado C es un camino cuyos extremos son el mismo vértice.
Definición 1.3.3: Sea G(V,A) un grafo; decimos que es conexo si para todo par de vértices v i y v j existe un camino entre v i y v j .
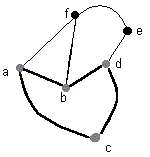 |
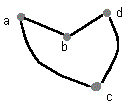 |
| Figura 1.3.3 Grafo Conexo H | Figura 1.3.4 Camino Cerrado del grafo H |
Cuando tenemos grafos no ponderados podemos suponer que todas las aristas valen uno. Entonces el largo de un camino toma relevancia ya que nos indica que tan cerca están un par de vértices. Esto nos sirve para decidir qué camino tomar para llegar de un vértice a otro de la manera más eficiente. Cabe destacar, que el camino de menor largo no siempre es la mejor opción cuando se trata de un grafo con valores ponderados.
Definición 1.3.4: Sea C un camino entre v1 y vn V en un grafo G(V,A). Definimos el largo del camino C como: el número de pasos que contiene.
La noción de un camino es de gran importancia, ya que muchos problemas se reducen a encontrar "caminos" o "rutas de salida" entre pares de nodos. Cuando hablamos de buscar el "mejor camino" para llegar de un punto a otro, es cuando tenemos la noción de distancia y por tanto camino. De igual modo, en ocasiones deseamos realizar un recorrido y terminar en el mismo punto de inicio (caminos cerrados). Por esa razón requerimos una definición de costo de un camino cuando tratamos con grafos ponderados.
Definición 1.3.5: El costo de un camino C en un grafo ponderado G, es la suma de los valores ponderados de las aristas que conforman el camino. Si denotamos por |C| al costo del camino C. Entonces:
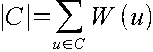
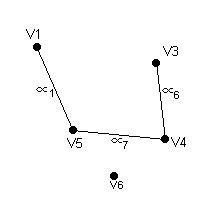
En la figura 1.3.6 tenemos un claro ejemplo de un grafo cuyo camino más corto, en pasos, no es el camino de menor costo ponderado. En este caso, pasando por c y e se tiene un costo de 16 mientras que pasar por b es un costo de 30.
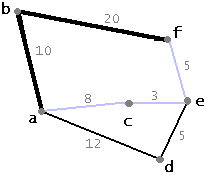
Figura 1.3.6. Grafo ponderado.
Cuando un grafo no tiene camino cerrados, se dice que es un árbol (quizás haciendo alución a las ramas que se forman por la forma de las aristas). Por lo tanto, los árboles son grafos simples ya que a lo más tienen una arista entre cada par de vértices. La figura 1.3.1 no es un grafo simple ya que tiene dos aristas entre los vértices v2 y v3. Por otro lado, el grafo de la figura 1.3.3 es simple al no repetir aristas.
Definición 1.3.6: Un grafo es simple si para toda pareja de aristas a y b, se cumple que ext(a) ¹ ext(b). Es decir, no hay dos aristas que compartan el mismo conjunto de vértices.
Definición 1.3.7: Un grafo se dice que es un árbol si no tiene caminos cerrados y es simple.
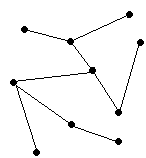
Figura 1.3.7. Ejemplo de árbol.
De las anteriores definiciones sobre grafo conexo y árbol, es posible deducir lo siguiente:
Proposicion 1.3.1: El grafo conexo de mínima cantidad de aristas, es un árbol
G(V,A) tal que |V| = n y |A| = n - 1. En otras palabras, el número de aristas es igual al número
de vértices menos uno.
Demostración:
Demostremos por inducción que la proposición es correcta.
Notemos que el mínimo grafo conexo de dos vértices contiene una arista (ignoremos el caso
trivial del grafo con sólo un vértice). Supongamos que la proposición es válida
en grafos de hasta n vértices. Entonces tomemos cualquier grafo
G(V,A) tal que |V| = n+1 vértices.
Para fines ilustrativos, imageninemos un grafo G como en la figura 1.3.8. De tal modo que sabemos que la
proposición es cierta hasta para n = 6.
Quitemosle un vértice cualquiera u y el conjunto B de las
aristas que tienen a u como uno de sus extremos.
En nuestro ejemplo quitemos g y las aristas que inciden en él.
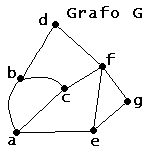
Figura 1.3.8. Grafo G de 7 vértices. |
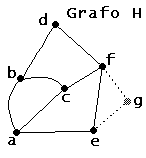
Figura 1.3.9. Grafo H de 6 vértices. |
Entonces el nuevo grafo H(V\{u},A\B) tiene n vértices (| V\{u} | = n ) y por tanto existe un
árbol conexo M(V\{u},C) tal que |C| = n - 1. Es decir, existe un árbol M que es conexo y une
a todos los vértices de H (ya que dijimos que era válido para grafos de hasta n vértices).
En la figura 1.3.10 podemos ver un árbol M a partir del grafo H.
Ahora tomemos este grafo M y agreguemos el vertice u y una arista del conjunto B (conjunto que tiene todas las
aristas donde alguno de los extremos es u). Entonces M sigue siendo un árbol pero de n+1 vértices
y con n aristas. Entonces por inducción es válido para toda n.
L.Q.Q.D.
Le figura 1.3.11 muestra el árbol construido a partir de M.
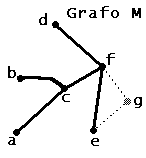
Figura 1.3.10. Árbol M de 6 vértices. |
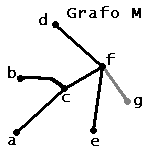
Figura 1.3.11. Árbol M agregandole g y una arista. |
Definicion 1.3.8: Un grafo completo es un grafo simple que tiene una arista entre cada par de vértices.
Un grafo completo tiene un total de [n*(n-1)]/2 aristas donde n es el número de vértices.
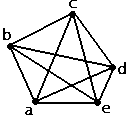
Figura 1.3.12. Grafo completo de 5 vértices.
Un viajero tiene una lista de n ciudades que quiere visitar. Entre esas ciudades hay un total de
m caminos que las conectan entre ellas. El viajero comienza en la ciudad a y quiere
regresar a ella al final de su travesia. Ayuda al viajero a determinar cuantas rutas diferentes hay. Una ruta
no debe visitar dos veces una misma ciudad (salvo la ciudad en la que inicia el viajero). Dos rutas se
consideran diferentes si visitan ciudades diferentes o en un orden diferente.
Input: La entrada viene en dos partes. La primera consiste en un grafo en formato 3.
La segunda, consiste en un único entero representando la ciudad a de inicio.
Output: Un sólo entero indicando el número total de caminos.
|
|
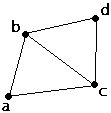
Figura 1.4.1. Grafo representado en el input 1.4.1.
Los arqueólogos han descubierto a la civilización OMInca y han localizado diversas ciudades. En una de las
excavaciones, descubrieron un papiro con geroglíficos extraños. Te han llamado (debido a tu
fama en resolver lenguas antiguas) para traducirlas. Al hacerlo, te percatas que es
una lista de ciudades representando un recorrido entre ciudades. La lista es tal que
entre dos ciudades contigüas, de la lista, debe existir un camino.
Te han dado la lista de todos los caminos, entre las ciudades OMIncas, que se conocen hasta ahora.
Tu trabajo consiste en determinar cuales caminos aún no se han descubierto (suponemos que todas
las ciudades se han descubierto).
Input: Consite en dos partes. La primera es un grafo en formato 3. La segunda consiste en dos
líneas, en la primera viene un solo entero 1 < k £ n que
indica el largo del camino escrito en el papiro y en la siguiente línea vienen
k enteros, separados por un espacio, que representan las ciudades que recorre el camino.
Output: El archivo debe contener tantas líneas como caminos no se hayan descibierto.
Los caminos deben estar en orden (según el orden del recorrido de la lista). Cada línea
debe contener un par enteros, separados por un espacio, indicando el camino que falta por descubrir.
|
|
En el planera Marte, han detectado n diferentes yacimientos de minerales ferrosos,
cada yacimiento tiene la misma cantidad de mineral.
Por ello, han mandado una sonda que es capaz de extraer el material de dos yacimientos exactamente.
La sonda puede llegar a cualquier yacimiento sin perdida de energia, pero una vez
que haya amartizado tiene que desplazarse al siguiente yacimiento por medio de sus ruedas (las cuales
consumen menos energia que despegar). La sonda debe buscar los dos yacimiento que se encuentran
lo más cerca posible, para gastar lo menos posible su energia, y retornar a la tierra.
La zona, en donde se encuentran los yacimientos, es totalmente plana y siempre es posible ir de un yacimiento
a otro en línea recta, por lo que el costo es siempre la distancia lineal entre los yacimientos.
Input: En la primera línea hay único entero 1 < n
£ 100, representando el número de ciudades y caminos en ese orden.
Posteriormente vienen n renglones. Cada renglón tiene dos enteros
-100 £ x £ 100 y
-100 £ y £ 100,
separados por un espacio, indicando las coordenadas de los yacimientos en formato (eje X,eje Y).
Output:Debe contener un único flotante, con dos decimales de precisión (sin redondeo),
que indica la distancia mínima a recorrer.
|
|
En Guanajuato hay muchos callejones que llevan a diferentes puntos de la ciudad.
Como buen explorador, te has dado a la tarea de ordenar los s callejones que salen
desde tu hotel. De este modo, en tu lista aparece, en primer lugar, el callejón más corto.
En segundo, el siguiente callejón mas corto y asi sucesivamente.
Has un programa que sea capaz de elaborar la lista a partir de un mapa dado y un punto k especificado.
Puedes suponer que las todas las aristas desde k tienen diferente valor.
Input:
La primera parte consiste en un grafo bidireccionado. Su entrada
viene en formato 2. Al terminar el grafo, en una nueva línea viene el entero k
Output: Debe contener s enteros. Cada entero xi
representa la existencia de la arista A(k,xi) y son tales
que ponderado W(k,xi) <
W(k,xi + 1).
|
|
Estadísticas
Última actualización:
Por Marte Ramírez