
2 Conceptos de caminos óptimos
2.1 Relajamiento de Caminos
2.2 Búsqueda Primero en Profundidad
2.3 Pseudocódigo BPP
2.4 Reconstruyendo el camino
2.5 Problemas
2.5.1 Paquetería
2.5.2 Paquetería II
Comúnmente, la necesidad de encontrar un camino óptimo entre dos puntos es de suma importancia. Por ello, en la teoría de grafos se han desarrollado diversos algoritmos de búsqueda en grafos ponderados. Dos de ellos, son presentados en este capítulo, ambos son algoritmos clásicos. Así pues, se pretende analizar su pseudocódigo y complejidad. Los algoritmos presentados funcionan para grafos direccionados o no direccionados, así como con aristas con diferentes ponderaciones dependiendo en que sentido es recorrido.
De ahora en adelante diremos que encontrar el "camino más corto" entre dos vértices equivale a poder obtener el camino entre los vértices cuyo costo es mínimo y por supuesto el valor de dicho costo. Cabe mencionar que a lo largo de este capítulo mostraremos pseudocódigos y analizaremos su complejidad respecto al modelo planteado. Por lo tanto, la complejidad varía, en gran medida, por el lenguaje que se emplea en su implementación como en su estructura de programación.
El saber qué ruta es la más corta, nos puede ayudar a determinar un mejor itinerario, una planeación de tiempo más conveniente o un ahorro de recursos. Desde luego, que esta aplicación en la importancia de ahorro de recursos se nota de manera más clara ante problemas de mayor complejidad como son: el recorrido del camión recolector de basura, en donde el tiempo y el ahorro de combustibles son de gran importancia. Del mismo modo, la búsqueda del camino más corto entre dos ciudades que tienen diferentes caminos con ciudades intermedias, las cuales tienen cada una su propio costo.
El anterior problema (muy sencillo de la vida real), nos obliga a determinar cual es la mejor opción de viaje entre dos ciudades distantes. Las diferentes escalas y costos (en muchas ocasiones no lineal). Nos hacen crear diversos algoritmos de búsqueda que nos minimice los costos de trasbordo y de pasaje.
En el siguiente problema también tenemos una situación similar: supóngase que tenemos una empresa dedicada a la seguridad de otras empresas. Para ello, dispone de vehículos blindados para el transporte de valor o vehículos de apoyo en llamadas de emergencia. Para esta empresa es necesario determinar cuál camino es más corto (lo que no necesariamente nos referimos a distancia) entre su base y cada empresa a la que presta servicios. Las consideraciones del peso de cada arista (que representan las calles), pueden variar entre su distancia, el tráfico según la hora del día, incluso el número de semáforos, pasos peatonales, etc. Todo lo anterior se puede resumir en tiempo aproximado de recorrido.
Nota:A partir de este momento supondremos que los grafos son ponderados, conexos, dirigidos y simples (salvo cuando indiquemos explicitamente otra característica). Es decir, todos los vértices estan conectados, las aristas son direccionadas con un valor ponderado y hay a lo más una arista entre cada par de vértices. Además supondremo que el conjunto de valores ponderados es W denotando w(u,v) el valor ponderado de la arista A(u,v).
Cuando hablamos del camino óptimo entre un par de vértices, no podemos hablar de un único camino sino de un conjunto de caminos (aunque en ocasiones el conjunto tiene un solo elemento) ya que pueden existir más de un camino óptimo. Por ejemplo, en el grafo de la figura 2.1, hay dos caminos óptimos entre el vértice a y d. Uno es pasando por b y el otro pasa por c. Por ello, será frecuente que hablemos del conjunto de caminos óptimos y cuando buscamos un camino óptimo, nos referimos a encontrar uno de ellos (mas no sabemos si hay más).
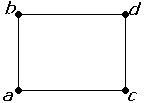
Figura 2.1.1.
Definición 2.1.1: Definimos como: CO(G,u,v) como el conjunto de caminos óptimos entre dos vértices u y v de grafo G. Cuando no haya ambiguedad con el grafo, simplemente lo denotamos como CO(u,v).
En muchos casos, hablaremos de un camino óptimo en particular. En nuestros algoritmos no encontraremos todos los caminos (salvo que sea un problema en particular), sino que buscaremos encontrar "alguno" de entre todos los que existen. Ese "alguno" lo manejaremos como el "representante" y nos servira como referencia para los calcular los costos o reconstruir la ruta óptima.
Notación 2.1.1: Denotamos como T(G,u,v) a algún elemento del conjunto CO(G,u,v). Es decir, es algún camino óptimo entre u y v. Cuando no haya ambiguedad con el grafo, simplemente lo denotamos como T(u,v).
Notación 2.1.2: El costo de un camino óptimo entre dos vértices u y v de grafo G lo denotaremos como: CCO(G,u,v). Cuando no haya ambiguedad con el grafo, simplemente lo denotamos como CCO(u,v).
En muchos ocasiones no se conoce el CC0(u,v) sino sólo algún valor que se puede haber tomado de alguna ruta cualquiera. Incluso, cuando no se conoce alguna ruta, se considera que el costo es infinito. Todos los algoritmos comienzan con un valor aproximado, del costo del camino deseado, el cual se ira mejorado hasta igualar el CCO. Por tanto, requerimos una notación que refiera a este costo aproximado.
Notación 2.1.3: Sea G(V,A) un grafo conexo. Denotamos como L(u,v) al costo del mejor camino encontrado, hasta el momento, entre u y v. L(u,v) toma el valor de infinito en el caso de no existir camino conocido entre dichos vértices.
Ahora veremos el concepto de relajamiento de camino. Imagina que, desde tu casa, sabes ir al cine por un camino que siempre has seguido y con el cual tardas 10 minutos. De igual modo, sabes llegar desde tu casa al supermercado en 4 minutos. Además el supermercado no queda de paso cuando vas al cine. Hace unos días mientras deambulabas por la ciudad, encontraste un camino que lleva del supermercado al cine y tardas t minutos. Ahora que conoces como llegar al cine desde el supermercado tienes un dilema. Qué camino será más corto para ir al cine? El viejo camino seguirá siendo más corto? O mejoras tu tiempo iendo al supermercado y luego seguir por el nuevo camino hacia el cine? La ruta casa-supermercado-cine tiene un costo de 4+t y la anterior era de 10. Si 4+t > 10 entonces es mejor la antigua ruta. Pero si 4+t < 10, entonces será mejor cambiar al nuevo camino que pasa por el supermercado. Recuerda que un camino está constituido por una o más calles. Es decir, no hablamos de un calle que lleve directamente al cine o al supermercado, sino de un camino que puede visitar diferentes lugares.
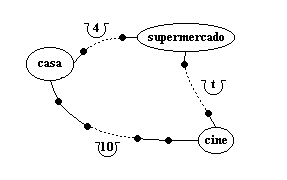
Figura 2.1.2. Escogiendo una mejor ruta.
En terminos formales; relajar el camino entre x y z equivale a escoger el mínimo costo entre el anterior costo L(x,z) y el nuevo posible costo L(x,y)+L(y,z). En otras palabras: L(x,z) = min(L(x,z),L(x,y)+L(y,z))
Este algoritmo emplea la búsqueda en profundidad. De todos los algoritmos que veremos, es el más ineficiente pero es bastante intuitivo y merece ser visto para fines educativos. La idea se basa en la búsqueda en profundidad y localiza el valor mínimo de un camino entre dos vertices dados.
Imaginemos que tenemos un grafo G como se muestra en la figura 2.2.1 cuyas aristas son bidereccionadas con peso igual a uno y queremos ir del punto a al punto f. De ahora en adelante visitaremos los vértices en modo alfabetico cuando tengamos que decidir que camino tomar.
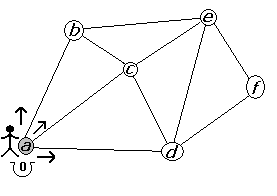
Figura 2.2.2
La primera alternativa para buscar el camino óptimo, es probar cada uno de los caminos posibles. Para ello, debemos recorrer todos las aristas que salen desde u. Recursivamente, para cada uno de los vertices adyacentes x, debemos explorar todos los caminos que llevan a v y que no pasen por u. A medida que nos metemos en la recursión debemos tener encuenta qué vértices hemos visitado para no repertirlos en nuestra visita.
Para fines ilustrativos, mostraremos la ejecución, paso a paso, de un caso de prueba. Nuestro objetivo será encontrar el costo del camino más corto entre el vértice a y f. En caso, suponemos que el costo de ir a cualquier vértice es infinito salvo el punto a cuyo costo es de cero.
 Figura 2.2.2 |
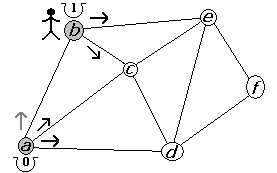 Figura 2.2.3 |
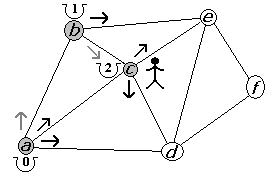 Figura 2.2.4 |
Desde a tenemos tres alternativas: b, c y d (figura 2.2.2). La primera alternativa, desde a, es visitar el punto b. Entonces, como b no se había visitado antes, el costo de llegar es 1. Ahora desde b tenemos dos opciones: c y e (figura 2.2.3). La primera alternativa, desde b, es c. Por lo tanto, el costo de llegar a c, desde b, es igual al costo de llegar a b (1) más el costo de la arista entre b y c, lo que da un total de 2. Ya estando parados en c tenemos dos opciones: d y e (figura 2.2.4).
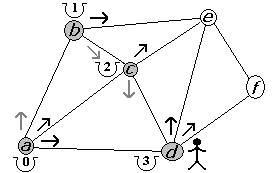 Figura 2.2.5 |
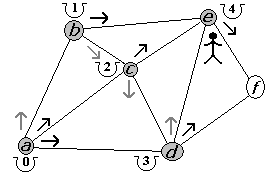 Figura 2.2.6 |
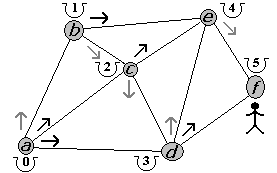 Figura 2.2.7 |
La primera alternativa, desde c, es d llegando con un costo de 3 (dos de llegar a c más uno de la arista entre c y d). Al igual que antes, desde d tenemos dos opciones: e y f (figura 2.2.5). La primera alternativa, desde d, es e llegando con un costo de 4. Desde e sólo tenemos una opción: f (figura 2.2.6). Por último, desde e solo podemos visitar a f (figura 2.2.7). Entonces, el camino fue {a, b, c, d, e, f} con un costo de 5, puesto que recorrimos 5 aristas.
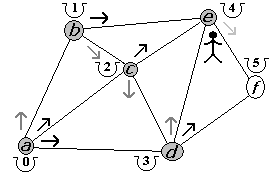 Figura 2.2.8 |
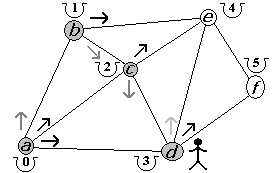 Figura 2.2.9 |
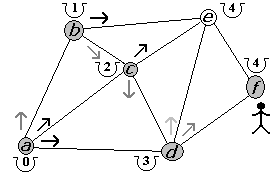 Figura 2.2.10 |
Como llegamos a nuestro destino, retornamos al punto e (figura 2.2.8). Desde e ya visitamos todas las opciones por lo que regresamos a d (figura 2.2.9). La segunda alternativa, desde d, es f (figura 2.2.10). Entonces, el camino fue {a, b, c, d, f}} con un costo de 4 (mejor que 5) puesto recorrimos 4 aristas.
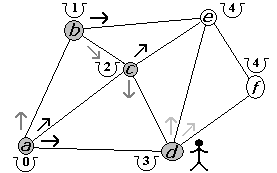 Figura 2.2.11 |
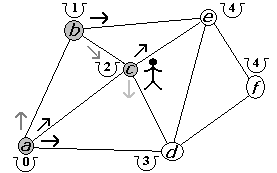 Figura 2.2.12 |
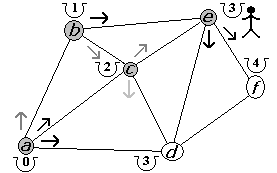 Figura 2.2.13 |
Retornamos al punto d (figura 2.2.11). Ahora en d ya visitamos todas las opciones por lo que regresamos a c (figura 2.2.12). Nuestra segunda alternativa, desde c, es visitar e. El costo anterior de llegar a e era de 4 por lo que nos conviene llegar a e desde c con un costo total de 3 (figura 2.2.13).
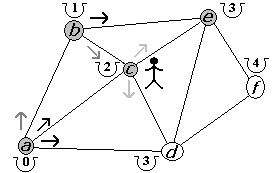 Figura 2.2.14 |
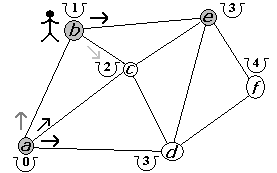 Figura 2.2.15 |
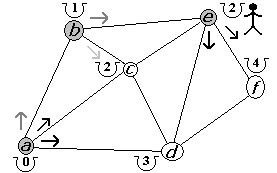 Figura 2.2.16 |
Observemos que desde e podemos llegar a d y f pero en ambos casos no mejoramos el costo de llegar a tales puntos, por ello, damos por terminada nuestra exploración desde e (figura 2.2.14). Al regresar a c hemos terminado de explorar todos sus caminos, por lo que retornamos a b (figura 2.2.15). La segunda y última opción, desde b, es ir a e y con el cual mejoramos su costo a 2 ya que anteriormente era de 3 (figura 2.2.16).
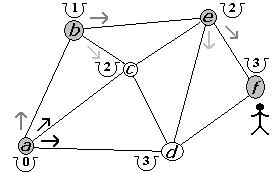 Figura 2.2.17 |
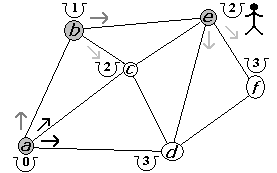 Figura 2.2.18 |
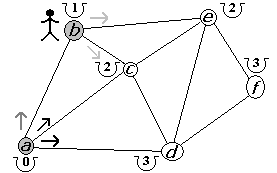 Figura 2.2.19 |
La primera opción es d. Sin embargo, no mejorariamos el costo, por lo tanto nos saltamos al segundo camino (hacia f). El costo para llegar a f desde e mejora, quedando en 3 (figura 2.2.17). Ahora retornamos a e (figura 2.2.18) para posteriormente retornar a b (figura 2.2.19).
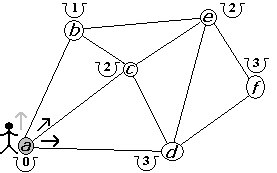 Figura 2.2.20 |
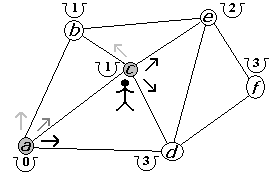 Figura 2.2.21 |
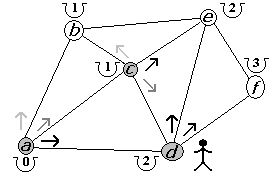 Figura 2.2.22 |
El segundo camino a escoger desde a es c. Entonces mejoramos el costo a 1 (anteriormente tenía un costo de 2) como vemos en la figura 2.2.20. A partir de c podríamos tratar de visitar b pero no tendríamos mejora en el costo (figura 2.2.21). por lo que seguimos con nuestra siguiente opción. Al ir a d, desde c, mejoramos a 2 nuestro costo (figura 2.2.22).
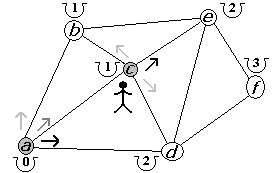 Figura 2.2.23 |
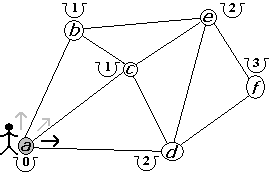 Figura 2.2.24 |
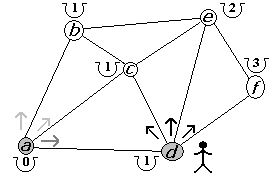 Figura 2.2.25 |
En d tenemos dos caminos a escoger. Sin embargo, en ambos casos no mejoramos no tendríamos alguna mejora en los costos. Por ello, damos por terminada la exploración en d y retornamos a c (figura 2.2.23). El tercer y último camino, desde c, es ir a e. Pero no logramos mejorar su costo por lo que terminamos en c y retornamos al punto a (figura 2.2.24). Al retornar al vértice a, tomamos nuestra última opción la cual es ir a d. En este caso, mejoramos su costo a 2 (figura 2.2.25).
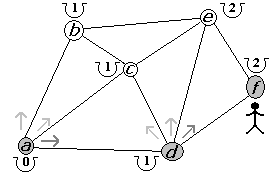 Figura 2.2.26 |
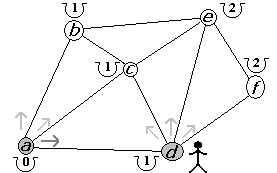 Figura 2.2.27 |
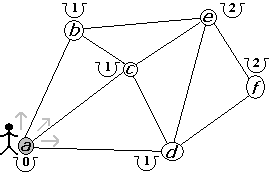 Figura 2.2.28 |
De los 3 posibles caminos, a partir de d, sólo obtenemos una mejora en el camino hacia f (figura 2.2.26). Al llegar a f actualizamos su costo a mínimo de 2 y damos por terminada la búsqueda y retornamos a d (figura 2.2.27). Al retornar a d hemos agotado todos los caminos por lo que retornamos a a y con ello, damos por terminada nuestra búsqueda (figura 2.2.28).
Este algoritmo sería idéntico a una simple búsqueda en profundidad si no le agregaramos una lista con el mejor costo que se tiene para cada vértice. Es decir, contamos con un listado del costo para cada vértice que hayamos visitado (se considera infinito si no se ha visitado) en algún paso de nuestro algoritmo. Esta lista nos sirva para "podar nuestra árbol de búsqueda".
Considere un grafo G(V,A) y el punto de inicio como ini.
costos: los costos de los vértices que llevamos hasta el momento.
destino: el vértice al cual queremos llegar.
verticeActual: el vértice en donde estamos parados en nuestro recorrido actualmente.
vertices: el conjunto de vértices que aún no han sido visitados.
w: la matriz de valores ponderados.
1 costos[i] <- para i = 1,2,...|V|
2 costos[inicio] <- 0
3 vertices <- V\{inicio}
4
5 bpp(vertices,verticeActual,destino,costos,w)
6 {
7 Si costos[verticeActual] > costos[destino]
8 finaliza
9
10 Para toda u en vertices
11 {
12 Si w(verticeActual,u) != INFINITO
13 {
14 Si costos[verticeActual] + w(verticeActual,u) < costos[u]
15 {
16 costos[u] <- costos[verticeActual] + w(verticeActual,u)
17 Si u != destino
18 bpp(vertices\{u},u,destino,costos,w)
19 }
20 }
21 }
22 }
|
Código 2.3.1. Pseudocódigo del bpp.
Al comparar el costo[verticeActual] contra el costo[destino] (línea 7) estamos evaluando si la exploración, por ese camino, debe continuar o no. Ya que no tiene caso seguir por un camino cuyo costo es igual o mayor al camino más corto encontrado (hasta el momento).
En la línea 12 nos cercioramos si existe la arista entre el vértice verticeActual y el vértice u. De ser el caso, tratamos de relajar la arista (verificamos si nos conviene llegar a u a través del camino que pasa por verticeActual) como se muestra en la línea 14. Por último, si la arista fue relajada y además el vértice u es diferente al destino, mandamos a llamar recursivamente a la función pero quitando a u del conjunto de vértices por visitar y pasando a u como verticeActual.
Desde luego que nos interesa conocer cuál es el costo mínimo para ir de un punto a otro. Pero también es necesario saber exactamente cuál es el camino a seguir. El proceso de reconstruir, el camino seguido, se basa en utilizar una lista (arreglo de enteros) que para cada vértice u contenga el vértice v que precede en su camino óptimo.
Digamos que T(a,b,c) denota un camino óptimo entre a y c que pasa por b. Entonces T(a,b,c) = T(a,b) + T(b,c) (suponiendo que el operador "+" une los caminos). Por lo tanto, podemos decir que si conocieramos el camino que va de a a b y de b a c, podriamos reconstruir el camino entre a y c.
Notación 2.4.1: Dado un camino T(a,b), denotamos C(b) como el último vértice visitado, siguiendo el camino T(a,b), antes de llegar a b. Consideramos C(a) = -1.
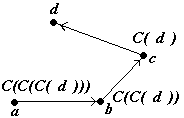
Figura 2.4.1. El camino entre a y d pasa por b y d.
En la figura 2.4.1 se puede se puede observar un camino entre a y d. El vértice c es el predecesor del vértice d. Por tanto C(d) = c. A su vez, el predecesor de c es C(c) = b. Sustituyendo se obtiene que C(C(d)) = b. Este proceso de sustitución lo podemos emplear para reconstruir todo nuestro camino, comenzando por nuestro destino y terminando en nuestro punto de partida. Entonces las aristas, del camino, quedarían como A(d,C(d)), A(C(d),C(C(d))),A(C(C(d)),C(C(C(d))))... hasta llegar a nuestro origen.
Consideremos las siguientes variables como:
verticeActual: vértice del camino sobre el cual estamos parado. inicialmente toma el valor
del destino.
predecesor: arreglo que contiene los predecesores de cada uno de los vértices.
camino: arreglo con el camino reconstruido, hasta el momento, desde el destino.
posCamino: variable que nos indica cuantos vértices tenemos en nuestro camino reconstruido.
1 recontruyeCamino(verticeActual,predecesor,camino,posCamino)
2 {
3 Si verticeActual == -1
4 {
5 imprime(camino,posCamino)
6 finaliza
7 }
8
9 camino[posCamino] = verticeActual
10 reconstruyeCamino(predecesor[verticeActual],predecesor,camino,posCamino+1)
11 }
|
Un repartidor de paquetes tiene una entrega urgente. Por ello requiere llegar lo
antes posible a su destino. Para fortuna de él, su empresa cuenta con un mapa detallado
de todas las calles de la ciudad asi como de los sentidos. Ayuda a determinar
el mejor camino entre su punto de partida u y el destino v de la entrega.
Input: La entrada consiste en dos parte. La primera consiste en un grafo direccionado en formato 2.
La segunda consiste en una línea con dos enteros que representan a u y v.
Output: Un sólo entero indicando el costo del camino mínimo entre u y v.
|
|
De nueva cuenta, un repartidor de paquetes tiene una entrega urgente. Por ello requiere llegar lo
antes posible a su destino. Desafortunadamente algunas esquinas estan totalmente cerradas por reparación
Ayuda a determinar el mejor camino, entre su punto de partida u y el destino v
de la entrega, sin pasar por algunos vértices marcados.
Input: La entrada consiste en dos parte. La primera consiste en un grafo direccionado en formato 2.
La segunda consiste en dos líneas, la primera contiene dos enteros que representan a u y v.
La segunda contiene un entero s seguido de s enteros que representan a los vértices que no
pueden visitarse.
Output: Un sólo entero indicando el costo del camino mínimo entre u y v.
|
|
Estadísticas
Última actualización:
Por Marte Ramírez