1. Divisibilidad
   • 1.1 Definiciones y Propiedades de Divisibilidad
   • 1.2 Primos
     • Problema 1: Primos
2. Máximo Común Divisor
   • 1.1 Definición y Propiedades del MCD
     • Problema 2: Algoritmo de Euclides
   • 1.2 Coprimos
     • Problema 3: Matemático Caprichoso
3. Mínimo Común Múltiplo
   • Problema 4: MCD
   • Problema 5: Fracciones Irreducibles
4. Congruencias
   • Problema 6: Coordenadas
5. Sucesiones
   • 5.1 Definición de Sucesión
   • 5.2 Notación Sigma
   • 5.3 Sucesión Aritmética
   • 5.4 Sucesión Geométrica
6. Criterios de Divisibilidad

1. Divisibilidad

1.1 Definiciones y propiedades de Divisibilidad

Cuando consideramos dos números naturales (nosotros consideraremos el cero también como natural), n y m, decimos que m divide a n, cuando existe otro entero positivo k tal que: n = m•k

En tal caso, decimos que n es un múltiplo de m y que m es un divisor de n. La notación m|n es empleada para indicar que m es divisor de n. Cuando un número no es divisor de otro lo denotaremos como m¦n. Para este caso es posible mostrar que existen un par único de naturales q y r tal que: n = m•q + r con 0 < r < m. Observemos que cuando n se divide entre m se tiene como cociente a q y como residuo a r.

Lista 1:Sea n, m, s, w, k naturales entonces se tienen las siguientes relaciones:

1. n|n para toda n (Es reflexiva).
2. n|0 para toda n.
3. Si n|m y m|n si y sólo si n = m.
4. Si n|m y m|s. Entonces n|s (Es transitiva).
5. Si n|m Entonces n|k•m para toda k. Esto es, divide a todos sus multiplos.
6. Si n|m y n|s. Entonces n|( k•m ± s•w).
7. Si n|m y n|( m ± s). Entonces n|s.

Ejercicios: Mostrar que las siguientes proposiciones no se cumplen para todos los números. Sea n, m, k naturales:

1. Si n|(m ± k). Entonces n|m ó n|k.
2. Si n|k•m. Entonces n|m ó n|k.
3. Si n|m•k. Entonces n|m.

1.2 Primos

Decimos que un número entero positivo p es primo si y sólo si p es mayor que 1 y los únicos divisores de p son: 1, p. Los números primos son muy estudiados por las propiedades peculiares que presentan. Entre ellas podemos enunciar el teorema fundamental de la aritmética que dice:

Teorema fundamental de la aritmética: Todo número que no es primo es compuesto y tiene una factorización única de primos salvo por permutaciones en el orden de los primos.

La Multiplicidad de un primo p en un número n es igual al número de veces que se encuentra p en la factorización de n. Esto es, si p^k|n y p^k+1¦n. Entonces la multiplicidad de p con respecto a n es de k. Por ejemplo la multiplicidad de 5 respecto al 90 es de 1 pero la multiplicidad de 3 es 2 ya que 60 = 2•3²•5

Teorema: El número de primos es un número infinito.
Demostración:

Supongamos que el número de primos es finito. Entonces hagamos una lista de los n primos existentes y ordenemos: p₁ < p₂ < p₃,... < p_n. Ahora sea m=p₁•p₂•...•p_n+1 . Notemos que p₁¦m, p₂¦m,... etc Entonces m es primo!!! lo cual es una contradicción pues dijimos que P_n era el primo mayor.

L.Q.Q.D

Lista 2: Sea n, m naturales y p primo. Entonces se tienen las siguientes relaciones:

1. Si p|n•m. Entonces p|n ó p|m
2. Si p¦n para toda p < raiz(n). Entonces n es primo
3. Si p^k|n y q^s|n con p≠q primos. Entonces p^k•q^s|n

La relación 1 aprovecha la propiedad de indivisibilidad de un número primo. De este modo, si un número k se puede expresar como multiplo de otros dos números n, m y si p|k entonces, p tiene qué ser divisor de al menos uno de los dos números.

De la relación 2 de la lista anterior se tiene un resultado en la busqueda de primos. "n" es primo si para todo primo p<raiz(n) p¦n (p no divide a n). Lo cual no a una cota para buscar los divisores primos de un número cualquiera y ver si es primo o no.

Con la tercera relación tenemos un hecho importante ya que si queremos demostrar que un número m divide a otro n. Basta demostrar que cada primo, con su debida multiplicidad, que divide a m también divide a n.

Problema 1: Primos

Escribir un programa que, para cualquier natural n dé una lista de todos los naturales primos menores o iguales que n.

Entrada (Archivo input.txt): Leer un único entero que indica el valor de n < 1,000,000

Salida (Archivo output.txt): Escribir en la primera linea un entero m que indique el número de primos seguido de m líneas con cada primo ordenados de menor a mayor.

Checa los Criterios de Divisibilidad

Indice

Máximo Común Divisor

2.1 Definición y propiedades del MCD

El Máximo Común Divisor o mcd de dos números n y m se define como el número más grande que es divisor tanto de n como de m. Se denota como (n,m). Siempre existe el mcd de dos o m´s números ya que le 1 es divisor de todos los naturales. En particular se tiene las siguientes propiedades:

Lista 3:Sea n > m, s, w, d números naturales y k = mcd(n,m)

1. Si d|n y d|m. Entonces d|k
2. k|( s•n ± w•m)
3. mcd(n,n) = n
4. Si n = m•s. Entonces mcd(n,m) = m
5. Si n = m•s + w con 0 < w < m. Entonces mcd(n,m) = mcd(m,w)

De la propiedad dos y tres tenemos un importante resultado del derivó el algoritmo de Euclides. Euclides pensó hace mucho tiempo un procedimiento para obtener el mcd de dos números naturales empleando la propiedad de k|(n - m). Observemos que mcd(n,m) = mcd(n-m,m) Con la diferencia de que si n - m < n

El Algoritmo de Euclides se basa en las propiedades 4 y 5. De este modo tenemos un algoritmo más eficiente que el algoritmo que emplea las propiedades 2 y 3.

Problema 2: Algoritmo de Euclides

Calcula el mcd de dos números naturales n < 1,000,000 y m < 1,000,000.
Problema A: Emplea las exclusivamente las propiedades 2 y 3.
Problema B: Programa el Algoritmo de Euclides empleando las propiedades 4 y 5.

Entrada (Archivo input.txt): Leer dos enteros separados por un espacio que indican el valor de n y m. No se sabe el orden de las variables. Es decir, no podemos suponer cual número es mayor.

Salida (Archivo output.txt): Escribir en la primera linea el mcd de n y m.

2.2 Coprimos

Decimos que dos números diferentes n y m son primos relativos o Coprimos si mcd(n,m) = 1. En otras palabras, n y m son primos relativos si para todo primo p tal que p|n se tiene que p¦m.

Lista 4: Sea n, m, s, p, q enteros.

1. mcd(n,m) = 1 si y sólo si n y m son primos relativos.
2. Si p^k|n y q^s|n con p≠q primos relativos. Entonces p^k•q^s |n.
3. Si k = mcd(n,m), n = d•s y m = d•w. Entonces s y w son primos relativos.

Problema 3: Matemático Caprichoso
Empleado como Problema 1 de la tarea 2 del entrenamiento 2003 de la OIEG
Problema original del VIII Concurso de la Olimpiada Mexicana de Matemáticas

Un matemático caprichoso tiene una forma curiosa de leer los libros. Primero lee la última hoja del libro (el libro tiene N hojas). después lee las hojas cuyos números son primos relativos a N (afortunadamente estas hojas las lee de menor a mayor). después busca la última hoja que no haya leido, digamos M, lee M y luego lee todas las hojas que cuyos números son primos relativos a M y así sucesivamente...

Escribe un programa que reciba como parámetros un entero N. N indica cuantas hojas tiene el libro. El programa debe de regresar un valor M tal que M es la última hoja leida.

Indice

Mínimo Común Múltiplo

El Mínimo Común Múltiplo o mcm de dos números n y m se define como el menor número que es múltiplo tanto de n como de m. Se denota como [n,m]. Siempre existe el mcd de dos o m´s números ya que le n•m es múltiplo de todos de n y m. En particular se tiene las siguientes propiedades:

Lista 5: Sea n > m, s, w, d números naturales y k = mcm(n,m)

1. Si n|d y m|d. Entonces k|d
2. mcm(n,n) = n
3. Si n = m•s. Entonces mcd(n,m) = n
4. Si n y m son coprimos. Entonces k = n•m

Un resultado importante se desprende de la relación que existe entre el mcd y el mcm ya que si d = mcd(n,m) y k = [n,m] Entonces d•k = n•m.

	Su demostración es la siguiente:
	
	Sea n = d•s y m = d•w. 
		Entonces:
		n•m = d•s•d•w = d•(d•s•w).
	
	Sea z = d•s•w. Demostremos que z = k
	
		Como s= d•s•w = n•w lo que implica que 
		n|z analogamente m|z. 
	
		Además si k = x•n = x•d•s = y•d•w; 
	
		lo que implica:
			x•s = y•w pero w es coprimo de s. 
		Entonces:
			 w|x y por lo tanto w•d•s;|x•d•s
	
	En conclusion z|k pero ya demostramos que z es múltiplo de n y m. 
	De lo anterior se tiene que k|z por lo tanto z = k. 
	

L.Q.Q.D

Problema 4: MCM

Calcula el mcm de dos números naturales n < 1,000,000 y m < 1,000,000.

Entrada (Archivo input.txt): Leer dos enteros separados por un espacio que indican el valor de n y m.

Salida (Archivo output.txt): Escribir en la primera linea el mcm de n y m.

Problema 5: Fracciones Irreducibles

Escribe un programa que dado un 0 < n < 100 fracciones calcule la suma y la exprese como una fracción irreducible

Entrada (Archivo input.txt):La primera línea contiene al entero n. Es seguido por n líneas. La línea (i+1) contiene dos enteros separados por un espacio que indican el valor del numerador y del denominador (en ese orden) de la fracción i. La respuesta siempre es una fracción.

Salida (Archivo output.txt):Debes escribir dos enteros separados por un espacio que determinan el numerador y denominador de la fracción.

Indice

Congruencias

Si tomaramos dividieramos todos los números naturales entre un número n y anotaramos sus residuos obtendríamos una lista como la siguiente:

0, 1, 2, 3, ... ,(n - 2), (n - 1), 0, 1, 2, ... ,(n - 2), (n - 1), 0, 1,...

Como podemos ver, tenemos una sucesión de recurrencia n. Cuando tomamos dos números cualesquiera a y b expresados en terminos de un número n y los sumamos tenemos la siguiente relación:

a = n•q₁ + r₁ con 0 < r₁ < n
y
b = n•q₂ + r₂ con 0 < r₂ < n

a + b = n•(q₁ + q₂ ) + r₁ + r₂

Entonces basta ver si r₁ + r₂ suman justamente "n" para determinar si n|(a + b). Luego es evidente que la suma de cualquier pareja de números cuyos residuos sumen n será multiplo de n. Ahora pensemos que n|(a + b) entonces cualquier c cuyo residuo sea igual a b cumplira con la propiedad de que n|(a + c). De aquí podemos observar una clara relación entre b y c ya son "relativamente equivalentes".

Dos naturales a y b son congruentes en modulo n si n|(a - b). En otras palabras, deben de tener el mismo residuo al ser divididos entre n. Se denota como a ≡ b mod(n). De este modo, 5 ≡ 16 mod(11) pero 5 ≡! 16 mod(10) (≡! denota que no son congruentes).

Lista 6: Sea a, b, c, d, s, w y n enteros

1. a ≡ a mod(n) para toda a (simétrica)
   
2. Si a ≡ b mod(n).
        Entonces
        b ≡ a mod(n) (reflexiva)
   
3. Si a ≡ b mod(n) y b ≡ c mod(n).
        Entonces
        a ≡ c mod(n) (transitiva)
   
4. Si a ≡ b mod(n).
        Entonces
        k•a ≡ k•b mod(n)
   Y también
        k•a ≡ k•b mod(k•n)
5. Si a ≡ b mod(n) y k|n.
        Entonces
        a ≡ b mod(k)
6. Si a ≡ b mod(n) y c ≡ d mod(n).
        Entonces
         s•a ± w•c ≡ s•b ± w•d mod(n)
   
7. Si a ≡ b mod(n) y c ≡ d mod(n).
        Entonces
        a•c ≡ b•d mod(n)
   

La propiedad 4 se puede demostrar de manera sencilla si expresamos a y b en términos de n. Como a ≡ b mod(n) sea r su residuo con 0 < r < n.

a = n•q₁ + r
y
b = n•q₂ + r

k•a = n•k•q₁ + k•r
Y
k•b = n•k•q₂ + k•r

Entonces: k•a - k•b = n•k•(q₁ + q₂ )
Por lo tanto n |(k•a - k•b)
Esto implica que k•a ≡ k•b mod(n)

L.Q.Q.D

Las propiedades 5, 6 y 7 de la lista 6, se pueden demostrar de la misma manera que la propiedad 4. Sin embargo, existen dos propiedades más que son de gran utilidad en la manipulación de residuos.

Si a ≡ b mod(n). Entonces a^k ≡ b^k mod(n).

La anterior propiedad se puede demostrar empleando la propiedad 6 de la lista 6 de manera recursiva n veces.

Si k•a ≡ k•b mod(n). Entonces a ≡ b mod(n/mcd(k,n))

Demostración:

	Sea d = mcd(k,n), k = d•s, n = d•w a = w•q1 + r1, b = w•q2 + r2 
	
	De arriba sabemos que s y w son coprimos.
	
	Por otro lado sabemos que: k•a ≡ k•b mod(n)
		Entonces: k•r1 ≡ k•r2 mod(n)
	
	Por tanto, d•s•r1 ≡ d•s•r2 mod(d•w) Lo que implica que:
		
		d•w|(d•s•r1 - d•s•r2)
		w|(s•r1 - s•r2)			
		w|(s•(r1 - r2))
		
		Pero w¦s por ser coprimos. Entonces w|(r1 - r2)			
	

L.Q.Q.D

Cabe mencionar que la congruencia no solo se emplea en números positivos. Podemos hacer uso con números negativos. Por ejemplo: 13 ≡ -3 mod(8) ya que 8|(13 - (-3)). Por otro lado, hay que recalcar que existen "n clases" básicas en modulo n que son: 0, 1, 2, ... , (n - 2), (n - 1). Para cualquier número "a" existe una 0 < r < n tal que a es congruente con r en modulo n. Por último enlistemos algunas afirmaciones falsas y que suelen causar confusión cuando se inicia el estudio de la aritmetica modular.

Ejercicios: Demostrar que las siguientes afirmaciones son falsas.

1. Si k•a ≡ k•b mod(n). Entonces a ≡ b mod(n)
   No se puede dividir por cualquier k.
2. Si a^k ≡ b^k mod(n). Entonces a ≡ b mod(n)
   No se puede sacar raiz por cualquier k.
3. Si a ≡ b mod(n) y b ≡ c mod(m). Entonces a ≡ c mod(m)
   No es transitivo con modulos diferentes.

Denotemos como % al operador residuo (En el lenguaje C, el operador % se emplea también para calcular el residuo). Entonces la notación a%n indica el residuo de a al dividirse entre n.

Son muchas las aplicaciones paralas congruencias, sin embargo una aplicación muy común en la computación es cuando se requiere emplear algún tipo de ciclo con n estados diferentes. Por ejemplo, si tenemos las 4 direcciones elementales: Norte, Este, Sur y Oeste. De tal modo que Norte puede ser representado como un 0, Este con el 1, el Sur con el 2 y el Oeste con el 3. Veamos el siguiente problema para tener una mejor idea de su aplicación.

Problema 6: Coordenadas
Problema 2 de la tarea 1 del entrenamiento 2003 de la OIEG

Estas en un plano coordenado y puedes mirar al Norte, Este, Sur y Oeste. Recibes 3 instruciones diferentes: "D" significa que giras 90 grados a tu derecha, "I" giras 90 grados a tu izquierda y "A" que significa que avanzarás. Después de una "A" siempre viene un número que son la cantidad de unidades que te desplazas a la dirección hacia donde estabas mirando.

Escribe un programa que reciba un conjunto de 0 < n < 100 instrucciones y regrese las coordenadas del punto en donde terminas después de las n instrucciones. Siempre inicias en (0,0) y mirando al norte.

Entrada (Archivo input.txt):La primera línea contiene al entero n seguido de un salto de línea. n representa que hay n instrucciones. La segunda línea contiene las n instrucciones separadas por un espacio. Después de la instrucción Avanza (A) siempre viene un entero 0 < k < 100 separado por un espacio.

Salida (Archivo output.txt):Debes escribir dos enteros separados por un espacio que determinan las coordenadas X y Y respectivamente, de la posición final después de seguir las n instrucciones.

	#include <stdio.h>
	
	///************************
	int Dir[4],Ver,Pasos,N;
	char Letra;
	FILE *Input,*Output;
	///************************
	
	int main()
	  {
	  // Abrimos el archivo de entrada en modo de lectura.
	  Input = fopen("input.txt","r+t");
	  
	  // Inicializamos con cero las variables ya
	  // que comenzamos en (0,0) y mirando al Norte.
	  for(int i = 0; i < 4; i++)
	    { Dir[i] = 0; }
	  Ver = 0;
	  
	  // Leemos la N.
	  fscanf(Input,"%d",&N);
	  
	  for(int i = 0; i < N; i++)
	    {
	    // Leemos una instrucción.
	    fscanf(Input,"%s",&Letra);
	  
	    // Checamos en que dirección nos movemos.
	    if( Letra == 'D' )
	      { Ver = (Ver + 1)%4; }
	    if( Letra == 'I' )
	      { Ver = (Ver + 3)%4; }
	  
	    // En el caso de avanzar sólo sumamos el entero
	    // en la dirección actual en la que estamos.
	    if( Letra == 'A' )
	      {
	      fscanf(Input,"%d",&Pasos);
	      Dir[Ver] = (Dir[Ver] + Pasos);
	      }
	    }
	  
	  // Cerramos el archivo de entrada.
	  fclose(Input);
	  
	  // Abrimos el archivo de salida en modo de escritura.
	  Output = fopen("Ouput.txt","w+t");
	  
	  // Imprimos la solución.
	  fprintf(Output,"%d %d",Dir[1] - Dir[3],Dir[0] - Dir[2]);
	  
	  // Cerramos el archivo de salida.
	  fclose(Output);
	  
	          return 0;
	  }
	

Indice

Sucesiones

5.1 Definición de Sucesión

Hablando informalmente, una sucesión es una regla que asocia un número a cada número natural 0, 1, 2, 3, 4, ...... , el número asociado a k se llama el "k-ésimo término" de la sucesión y se lo indica con a_k. A menudo, se indica un sucesión escribiendo sus primeros términos; en tal caso, se supone que la regla para formar el "término general", es decir, el k-ésimo término para cualquier k, es clara. Por ejemplo:

(a) 0, 2, 4, 6, 8, 10, ....

(b) 1, 3, 5, 7, 9, ....

(c) 1, 0, 1, 0, 1, ....

(d) 1, 1, 2, 6, 24, 120, ....

(e) 1, 1, 2, 3, 5, 8, 13, ....

En nuestros ejemplos:

a_k = 2•k

b_k = 2•k + 1

c_k = [1+(-1)^k]/2

d₀ = 1 y d = k•d_k-1 si k > 1

e₀ = 1, e₁ = 1 y e_k = e_k-1 + e_k-2 si k > 2

Cuando, como en el caso de las dos últimas sucesiones, para conocer el valor de a_k se hace necesario conocer el valor de uno o más de los términos anteriores se habla de fórmulas de "recurrencia".

La sucesión del ejemplo (d) es la que define el factorial de k (k!) y la del ejemplo (e) es la famosa sucesión de Fibonacci.

Planteamos entonces dos ejercicios:

(A) Escribir un programa que permita el ingreso de un número natural n y que calcule n! exhibiendo el resultado.

(B) ídem (A) para la sucesión de Fibonacci.

5.2 Notacón Sigma

La Notación Sigma es empleada frecuentemente para indicar la suma de una sucesión de términos. Supongamos que tenemos una sucesión de la siguiente manera:

f(0), f(1), f(2),... f(n),... y queremos expresar s = f(n) + f(n+1) + ... + f(m-1) + f(m)

Entonces la notación sigma nos abrevia de la siguiente manera:

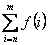
Donde la f representa la función de la sucesión cuyos elementos estamos sumando, la i varía entre los valores n y m que estan indicados en la parte inferior y superior de la sigma respectivamente.

Dos propiedades importantes son:

• Distribuye la suma y resta de funciones:
     
• Saca constantes de la sigma:
     
• No distribuye la multiplicación:
     

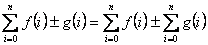
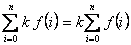
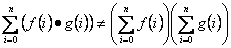
Algunas fórmulas conocidas son las siguientes:

• Suma de una constante k:
     
• Suma de los primeros n enteros positivos:
     
• Suma de los primeros n cuadrados:
     

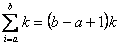
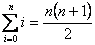
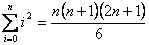
Ejercicios: Los primeros dos pueden ser resueltos facilmente empleando las propiedades de la notación sigma. Por otro lado, el tercer ejecicio requiere una buena dosis de ingenio.

1. Suma de los primeros n pares:
      
2. Suma de los primeros n impares:
      
3. Suma de los primeros n cubos:
      

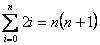
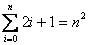
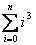
Sugerencia para el ejercicio 3: Observa la diferencia de dos cubos consecutivos y expresala en terminos cuadráticos, lineales y constantes. Has una lista de las diferencias y suma las diferencias de cubos.

5.3 Sucesión Aritmética

Una de las suceciones más comunes es precisamente la Suceción Aritmética. Esta se define para cada elemento, como la suma del elemento anterior más una constante. En termines de funciones podemos describirla como:

f(0) = a y f(i+1) = f(i) + r, para toda i > 0 y r constante.

la sucesión quedaría como: a, a + r, a + 2r, a + 3r,... ,a + nr,...

Es fácil determinar entonces que la suma de los primeros n términos es: a•n + r•n•(n-1)/2.

5.4 Sucesión Geométrica

La Suceción Geométrica se define para cada elemento, como el producto del elemento anterior con una constante constante. En termines de funciones podemos describirla como:

f(0) = a y f(i+1) = f(i)•r, para toda i > 0 y r constante.

la sucesión quedaría como: a, a•r, a•r², a•r³,... ,a•rⁿ,...

Ejercicio: Demostrar que la suma de los primeros n términos es: a•( (rⁿ - 1)/(r - 1) ).

Indice

Criterio de Divisibilidad

• Un número es divisible por 2 si su última cifra es par
• Un número es divisible por 3 si la suma de sus dígitos es multiplo de 3
• Un número es divisible por 4 si el número formado por sus 2 últimas cifras es multiplo de 4
• Un número es divisible por 5 si termina en 0 o 5
• Un número es divisible por 6 si lo es por 2 y 3
• Un número es divisible por 9 si la suma de sus dígitos es multiplo de 9
• Un número es divisible por 11 si la diferencia de la suma de los dígitos de lugar par y la suma de los dígitos de lugar impar, es multiplo de 11

Planteamos entonces dos ejercicios:

Indice