Primero se tiene que calcular el numero en el que se trunca el kernel, esto es, calcular el entero máximo n que satisface:
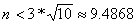
Por lo que basta tomar n=9. Por lo tanto, el tamaño del kernel es
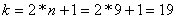 y el ahorro computacional
es de
y el ahorro computacional
es de 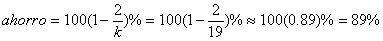 .
.
void conv(float **f,float **g,float *h1,int nh1,float *h2,int nh2,int nr,int nc)
{
float **nuevo;
int i;
nuevo=new float*[nr];
for (i=0;i<nr;i++)
{
nuevo[i]=new float[nc];
ConvR(f,nuevo,h1,nh1,nc,i);
}
for (i=0;i<nc;i++)
{
ConvC(nuevo,g,h2,nh2,nr,i);
}
for (i=0;i<nr;i++)
delete[] nuevo[i];
delete[] nuevo;
}
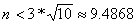
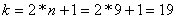 y el ahorro computacional
es de
y el ahorro computacional
es de 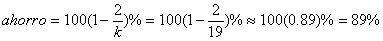 .
.

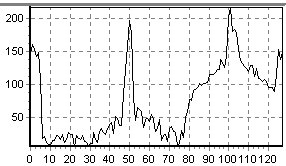

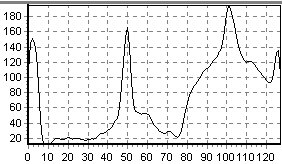




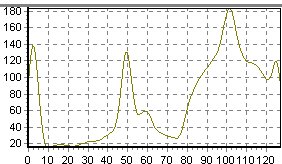
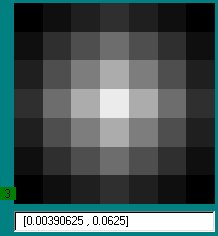

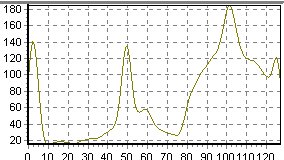
| Orden 1 | ||
|---|---|---|
| x | 0 | 1 |
| h(x) | 1 | 1 |
| Orden 2 (h*h) | |||
|---|---|---|---|
| x | 0 | 1 | 2 |
| sum h(i)h(x-i) | h(0)h(0-0)=1 | h(0)h(1-0)+h(1)h(1-1)=1+1=2 | h(1)h(2-1)=1 |
| Orden 3 (h2*h) | ||||
|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 |
| sum h2(i)h(x-i) | h2(0)h(0-0)=1 | h2(0)h(1-0)+h2(1)h(1-1)=1+2=3 | h2(1)h(2-1)+h2(2)h(2-2)=2+1=3 | h2(2)h(3-2)=1 |
| Orden 4 (h3*h) | |||||
|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 |
| sum h3(i)h(x-i) | h3(0)h(0-0)=1 | h3(0)h(1-0)+h3(1)h(1-1)=1+3=4 | h3(1)h(2-1)+h3(2)h(2-2)=3+3=6 | h3(2)h(3-2)+h3(3)h(3-3)=3+1=4 | h3(3)h(4-3)=1 |
| Orden 5 (h4*h) | ||||||
|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| sum h4(i)h(x-i) | h4(0)h(0-0)=1 | h4(0)h(1-0)+h4(1)h(1-1)=1+4=5 | h4(1)h(2-1)+h4(2)h(2-2)=4+6=10 | h4(2)h(3-2)+h4(3)h(3-3)=6+4=10 | h4(3)h(4-3)+h4(4)h(4-4)=4+1=5 | h4(4)h(5-4)=1 |

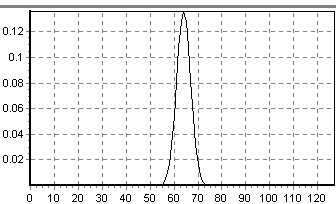
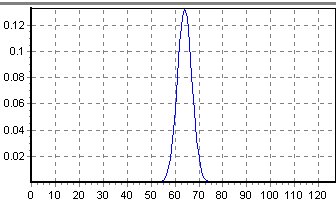
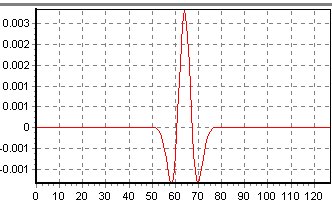
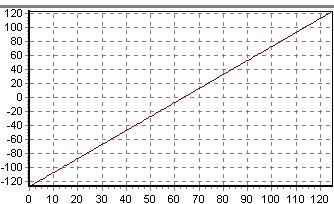
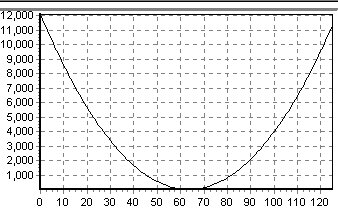
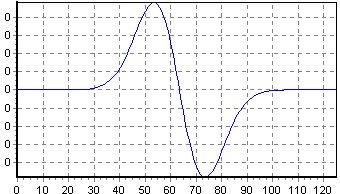
| Función | Derivada |
|---|---|
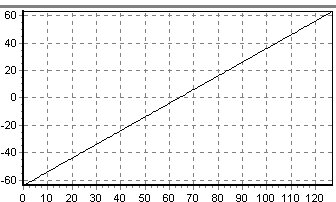 | 
|
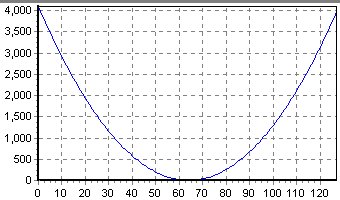 | 
|
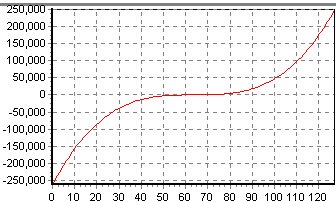 | 
|
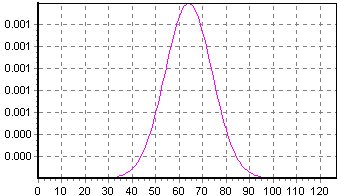 | 
|

| 2 | -2 | 1 |
| -2 | 0 | 0 |
| 1 | 0 | 0 |
