SOLUCIONES AL EXAMEN DE PRÁCTICA 1

ADVERTENCIA: Si intentas imprimir esta página, es bastante probable que no obtengas los resultados deseados, puesto que el texto está en color blanco. Si quieres ver una versión más favorable para la impresión, haz click aquí

Solución 2.
Notemos que si sacáramos 20 canicas podría ser que todas fueran de colores distintos, así que sólo podríamos garantizar que hay dos canicas del mismo color si sacáramos 21 canicas. De la misma manera, necesitaríamos 41=20 x 2 + 1 canicas para poder afirmar que con seguridad hay 3 canicas (al menos) del mismo color, pues con 40 canicas podría ser que cada color apareciera exactamente 2 veces. Con el mismo razonamiento que hemos seguido llegamos al resultado: se necesitan 20 x 99 + 1=1981 canicas. La respuesta es (c).

Solución 3.
Observemos que si juntamos los triángulos ABM y DNC, éstos formarán un rectángulo de 2.5 x 3, y que el área de MPQD es la mitad del área restante MBND para el rectángulo total, esto es: 5 x 3 - (2.5 x 3/2)=3.75. La respuesta es (d).

Solución 4.
En el primer paso, por cada 100 tendremos 110, a los cuales habrá que restarles 11 y, por tanto, nos quedaremos con 99. La respuesta es (b).

Solución 5.
Junto al 3 y al 5 hay que escribir dos números que sumen 12. Como no puede haber repeticiones, la única posibilidad para esos dos números es 8 y 4 (con dos posibilidades para ponerlos). Ahora, junto al 5 y al 8 hay que escribir números que sumen 20-(5+8)=7. Para evitar repeticiones las únicas posibilidades son 1 y 6. De la misma manera, vecinos al 5 y al 4 debemos escribir 2 y 9. Ahora, una vez que se ha elegido la forma de escribir el 4 y el 8, hay 4 posibilidades para escribir los números 1 y 6 y 2 y 9, pero sólo una funciona, ya que los cuatro números en la esquina izquierda superior deben también sumar 20. En resumen, sólo hay dos posibilidades:

La respuesta es (d).

Solución 6.
Del centro de los círculos tracemos segmentos a los puntos de tangencia del círculo menor con el cuadrado; así el cuadrado quedará dividido en cuatro cuadrados de lado 1, y el radio del círculo mayor será igual a la diagonal de cualquiera de ellos. Usando Pitágoras deducimos el resultado. La respuesta es (b).

Solución 7.
La longitud de AB es la suma de la longitud del lado mayor y la del lado menor de uno de los rectángulos pequeños. Sabemos que los tres rectángulos pequeños son iguales, por lo cual el lado más chico de cada uno de ellos mide la mitad de AD, que es igual a la mitad de BC y por tanto es 1. Luego, AB=2+1=3. La respuesta es (b).

Solución 8.
Conviene escribir los números como x-2, x y x+2. Entonces su suma es, por un lado, 3x y, por el otro, 27, de donde x=9. El más pequeño es 7. La respuesta es (d).

Solución 9.
El área del cuadrado ABCD es igual a 1 m² (cada lado del cuadrado mide 1 m). El área del cuadrado AKPC es igual a cuatro veces el área del triángulo ABC, cuya área es la mitad del cuadrado ABCD. El área de ABCD es igual a 0.5 x 4 m² =2 m². La respuesta es (c).

Solución 10.
Tenemos que 4321 - 1234 = 3087. La respuesta es (d).

Solución 11.
Es claro que una recta interesecta a lo más dos veces a un círculo, así que el máximo número de intersecciones en total entre el cuadrado y el círculo no puede exceder 8. En la figura siguiente podemos observar que sí es posible conseguir 8 puntos de intersección con un círculo de radio 5 y un cuadrado de lado 8 que compartan el centro. La respuesta es (d)

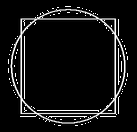
Solución 12.
Cada lado del cuadrado gris mide la tercera parte del cuadrado grande, así que el área del cuadrado es 1/3 x 1/3= 1/9 veces el área del cuadrado mayor. La respuesta es (b).

Solución 13.
Tenemos 50 números que podemos agrupar de dos en dos: (99-97)+(95-93)+...+(3-1). Cada paréntesis contribuye en 2 a la suma, así que la respuesta es 25 x 2=50. La respuesta es (d).

Solución 14.
Como 15 x 24 = 360 y 375 = 360 + 15, el asiento número 375 es el 15 de la fila 16. La respuesta es (e).

Solución 15.
Notemos que 350 pesos son 35 entradas de adultos, pero 50 personas implican 15 personas más. Si "cambiamos" un adulto por 2 niños, conservamos la cantidad (en pesos) pero aumentamos una persona más cada vez. Así, "cambiando" 15 adultos por 30 niños obtenemos 50 personas, y conservamos los 350 pesos de ganancias. (De otra manera: Llamemos n al número de niños y a al número de adultos. Entonces n+a=50  y 5n+10a=350. Dividiendo la segunda ecuación entre 5 y restándole la primera tenemos que a=20. La respuesta es (b).

Solución 16.
Si cortamos una esquina del triángulo de forma que el corte NO se haga por la diagonal del cuadrado, tendremos cinco esquinas en lugar de cuatro en la región más grande. Esto quiere decir que al cortar una esquina del cuadrado, lo más que podemos hacer es agregar otra. Así pues, el máximo de esquinas que podemos tener es 8. La respuesta es (e).

Solución 17.
La posición original se repite después de cada 6 dobleces. Como 1998 es múltiplo de 6, después de 1998 dobleces tendremos la posición original y después de 1999 dobleces tendremos la misma posición que había después del primer doblez.
La respuesta es (d).

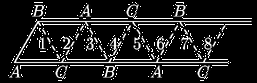
Solución 18.
Un rectángulo, como se observa en la figura. La respuesta es (b).

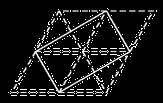
Solución 19.
En dos horas el entrenador lava 3 elefantes y su hijo lava 1, así que juntos lavan 4 elefantes en 2 horas y lavarán 3 elefantes en 3 x 2/4 = 1.5 horas. La respuesta es (d).

Solución 20.
El área de la rebanada es proporcional al ángulo comprendido entre los radios. Así, cuando el ángulo es de 360^o, el área de la rebanada es igual a la del pastel. Entonces, para que el sector sea el 15 % del área del círculo, el ángulo debe medir 15 % de 360^o: 54^o. La respuesta es (c).