
MaterialFolleto 10ª OMM-MICH
1. La figura (a) representa dos cuadrados que miden 11 m ×11 m y se traslapan para formar un rectángulo de 11 m ×18 m. Hallar el área de la región sombreada (en la que los dos cuadrados se traslapan). 2. Con 48 cubitos de madera se quiere formar una pirámide de tres niveles de tal forma que el segundo nivel tenga el doble de cubitos que el primero, y el tercer nivel tenga el triple que el primero. ¿Cuántos cubitos debe tener el segundo nivel? (Nota: Todos los cubitos deben ser utilizados para formar la pirámide.) 3. Un juego de dominó extraño tiene fichas con los números del 1 al 8 en cada uno de sus dos lados. (Por ejemplo, cuatro de esas fichas son 2|8, 3|3, 4|1, y 4|2 ¿Cuántas fichas tiene el juego en total si tiene todas las combinaciones de números del 1 al 8?. (Nota: Las fichas como 2|8 y 8|2 deben contarse una sola vez pues se consideran iguales.) 4. A un cubo sólido de 2 cm de lado se le quitan todos sus picos a una distancia sobre cada arista de 1 cm. (En la figura (b) se ilustra por dónde se cortaría uno de los picos.) ¿Cuántos vértices tiene la nueva figura? 5. A Juan se le olvidó el número secreto que le daba acceso al gimnasio; sin embargo, previendo su olvido anotó en su libreta los siguientes datos: La suma de los cuatro dígitos del número es 9 y ninguno de ellos es 0; además el número es múltiplo de 5 y mayor que 1995. ¿Cuál es el número? 6. ¿Cuántos ceros hay al final de
7. Se quiere cortar la figura de papel dibujada en la figura (c) en cuatro figuras idénticas y semejantes a ella. Marcar con líneas en el dibujo los lugares por dónde debería cortarse. 8. En cierto planeta hay tantos días en una semana como semanas en un mes como meses en un año. Si un año tiene 1331 días, ¿cuántos días tiene cada semana?
9. En la figura (d) aparecen los 36 vértices de una cuadrícula que representa 5 cm×5 cm. Usando esos puntos como extremos, ¿cuántos segmentos de 2 cm de longitud se pueden trazar? 10. Ana y Beto van a hacer un mismo recorrido de 120 km por carretera. Ana viaja a una velocidad constante de 80 km por hora y Beto viaja a una velocidad también constante de 60 km por hora. Si salen del mismo lugar (pero no al mismo tiempo) y se encuentran a la mitad del recorrido, ¿cuántos minutos antes salió Beto que Ana?
11. En la figura (e) ABCD es un rectángulo y P es un punto sobre el lado AB tal que el ángulo ÐDPC es recto y las longitudes de los segmentos PA, PD y PC son (en centímetros) las indicadas en la figura. Hallar el área (en cm2) del triángulo PBC. 12. Los enteros positivos se escriben en orden sucesivo por renglones según la siguiente regla: En el primer renglón va únicamente el 1; después, a partir del segundo renglón, en cada renglón se escribe doble cantidad de números que en el renglón anterior. (Para ilustrar, en la figura (f) se escribieron los tres primeros renglones.) ¿En qué número de renglón queda escrito el 1995?
13. Considera todos los números de 4 cifras que se forman usando sólo 1¢s y 2¢s. (Por ejemplo 1111, 2112 y 2122 son tres de esos números.) ¿Cuál es la cifra de las unidades de la suma de todos ellos? 14. En un cubo sólido de 4 cm de lado se hace una perforación en forma de prisma recto con base cuadrada de 1 cm de lado desde el centro de cada cara hasta su cara opuesta. (En la figura (g) se ilustró una de las perforaciones; hay que hacer dos perforaciones más usando las otras parejas de caras opuestas.) ¿Cuántos centímetros cúbicos de volumen tiene el nuevo sólido? 15. En las casillas de la cuadrícula (h) de la figura se van a escribir los números enteros del 1 al 9 (uno en cada una, sin repetir). Queremos que alrededor de cada vértice marcado con una flecha la suma de los cuatro números que queden sea 20. Si escribes 5 y 3 como se indica, ¿qué número deberá quedar en la casilla sombreada? 16. ¿Cuál es la cifra decimal que ocupa el lugar 1995 en el desarrollo decimal de [4/101]? (Por ejemplo, en el desarrollo decimal de p = 3.14159¼, las cifras decimales son las que aparecen a la derecha del punto decimal y los lugares que ocupan son: el lugar 1 lo ocupa el 1, el lugar 2 lo ocupa el 4, el lugar 3 lo ocupa el 1, etc.) 17. La resta de los cuadrados de dos números enteros positivos no consecutivos es 93. ¿Cuál es el mayor de esos dos números?
18. En la figura (i) RSTU representa un rectángulo de 24 cm ×18 cm; K es un punto sobre el lado RS y L es un punto en el interior del rectángulo de tal manera que el segmento KL es perpendicular a RS y los segmentos KL, UL y TL tienen todos tienen la misma longitud x. ¿Cuántos centímetros mide x?
19. En la figura (j) ABCDE representa un pentágono regular (de 1 m de lado) y ABP es un triángulo equilátero. ¿Cuántos grados mide el ángulo ÐBCP? 20. Prueba que todo cuadrado se puede cortar en 6 cuadrados, en 7 cuadrados, en 8 cuadrados y en 11 cuadrados. (Nota: Los cuadrados en los que partas no tienen que ser iguales entre sí. Para cada uno de los cuatro casos, dibuja un cuadrado e indica ahí con líneas por dónde harías los cortes; por ejemplo si te hubiéramos pedido que probaras que todo cuadrado se puede partir en 4 cuadrados, tu dibujo podría haber sido el de la figura (k).) [Problema propuesto por Jorge Luis López.] 21. En una ocasión se le preguntó al matemático Alfa que cuántos alumnos había tenido en las tres universidades donde había dado clases antes de retirarse. Alfa contestó: ``Sólo recuerdo que en la primera universidad donde trabajé tuve la décima parte de los alumnos que he tenido, en la segunda tuve varios séptimos del total y en la tercera universidad tuve 399 alumnos.'' ¿Cuántos alumnos tuvo Alfa en total? [Problema propuesto por Lorge Luis López.] 22. Se escriben en sucesión todos los números del 1 al 1995, en orden, uno a continuación del otro, para formar un número muy grande que llamaremos G (es decir, G = 1234567891011¼941995) ¿Cuál es la cifra central de G? y ¿a qué número de los de la sucesión corresponde esa cifra?
|
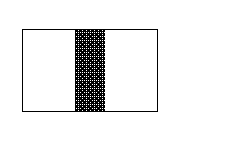 Figura (a)
Figura (a) 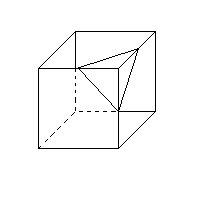 Figura
(b)
Figura
(b)  Figura (c)
Figura (c) Figura (d)
Figura (d)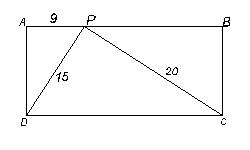 Figura (e)
Figura (e) 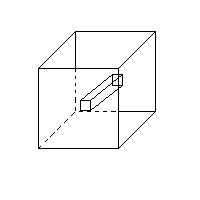 Fig (g)
Fig (g) 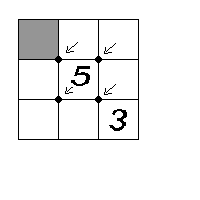 Fig
(h)
Fig
(h) 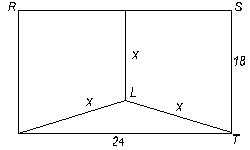 Fig (i)
Fig (i)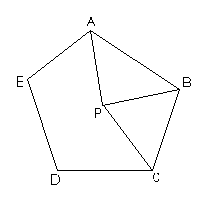 Figura (j)
Figura (j)  Figura
(k)
Figura
(k)