Material

Los siguientes 8 problemas formaron el Examen de Práctica de Michoacán de la 6^a Olimpiada Mexicana de Matemáticas. Se aplicó en algunas preparatorias del Estado y no tuvo ningún valor oficial. El tiempo para resolverlo fue de 1:00 h. Se calcula que 5000 alumnos de 1^o y 2^o años presentaron dicho examen, aunque la Escuela de Físico-Matemáticas de la Universidad sólo recibió el reporte de los resultados de 2470. Dentro de este grupo, 145 participantes obtuvieron al menos la mitad de las respuestas correctas; considerándose ésta una buena calificación para el tipo de examen de que se trataba, se invitó de manera muy especial (aunque no exclusiva) a esos alumnos y se publicó una lista con sus nombres y calificaciones. Para la aplicación de ese examen de práctica y su calificación se contó con la colaboración de algunos profesores de matemáticas de las mismas escuelas donde se aplicó el examen así como los alumnos de la Escuela de Físico-Matemáticas Edit Adan y Carlos Arce, quienes cubrieron con este trabajo su servicio social.

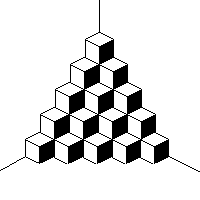
1. Un pastel se corta quitando cada vez la tercera parte del pastel que hay en el momento de cortar. ¿Que fracción del pastel original quedó después de cortar tres veces?

2. Se colocan unos cubos idénticos en un rincón de un cuarto como se muestra en la figura (A). ¿Cuántos cubos no son visibles?

Figura (A)

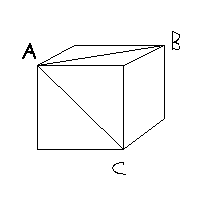
3. ¿Cuál es el menor entero positivo por el que se debe multiplicar 504 para obtener un cuadrado perfecto?

4. En una tarea Alberto sacó 80 de calificación y así elevó su promedio de 68 a 69. ¿Cuántas tareas había antes de esa última?

5. ¿Cuántos puntos de una circunferencia equidistan de dos rectas si las dos rectas son tangentes a la circunferencia y paralelas entre sí?

6. Si los números Ö5, ³ Ö{9}, 1, 2 y 3 se ordenan de izquierda a derecha en orden de magnitud, ¿cuál de ellos queda enmedio?

7. Un número palíndrome es un número entero que se lee igual de izquierda a derecha que de derecha a izquierda (por ejemplo 3808083). ¿Cuántos números palíndromes hay entre el 10 y el 1000?

8. Se trazan dos diagonales AB y AC de los lados de un cubo como se muestra en la figura (B). ¿Cuántos grados mide el ángulo BAC?

Figura (B)

Los siguientes 5 problemas formaron parte de la primera etapa del Examen Michoacano de la 6^a Olimpiada Mexicana de Matemáticas. Su duración fue de 3 h.

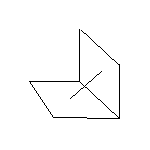
9,i) En el espacio se encuentran dos cuadrados de lado 2 con un lado común y perpendiculares. Hallar la longitud del segmento de recta que une los centros de los cuadrados. (Ver figura (C).)

Figura (C)

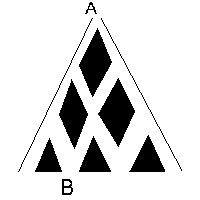
9,ii) Hallar el área de un triángulo equilátero de lado 2, y también el área de un triángulo equilátero de lado k.

9,iii) En un cubo de arista 20 están unidos, mediante segmentos de recta, los centros de cada par de caras adyacentes. Describe el poliedro que tiene por aristas esos segmentos y calcula el área de su superficie.

10. Calcular la suma de los 100 quebrados que se obtienen formando todos los cocientes de cada par de números de la siguiente lista

Nota: También deben tomarse en cuenta los quebrados en que numerador y denominador son iguales como [16/16].

Los incisos de la pregunta 11 se basan en la figura (D), la cual representa un juguete en el que se colocan pelotas por arriba (entrada A) y éstas van distribuyéndose por los caminos hacia abajo. En cada bifurcación la distribución de las pelotas obedece la siguiente regla: La primera que llega a la bifurcación toma la dirección hacia la izquierda: (hasta la siguiente bifurcación); las siguientes 2 pelotas toman el camino hacia la derecha (también hasta la siguiente bifurcación); la 4ª pelota va a la izquierda y las siguientes 2 a la derecha; así sucesivamente van alternándose 1 hacia la izquierda y 2 hacia la derecha.

11,i). Supongamos que se colocan 120 pelotas en la entrada A. ¿Cuántas pelotas saldrán por B?

11,ii). Decir una cantidad de pelotas que pueden haber entrado por A si se sabe que el número de pelotas que salieron por B es 50.

Figura (D)

12. Encontrar un entero positivo a tal que la suma

resulta ser un número con todas sus cifras iguales.

13. Se tienen 3 engranes A, B y C que tienen 12, 20 y 14 dientes, respectivamente. Empiezan los 3 en su pocición inicial, los 3 engranes juntos, de tal manera que cuando B gira, los otros 2 giran tambien. El engrane B gira en el sentido de las manecillas del reloj, avanzando un diente cada segundo. Calcular el tiempo que tardan los engranes en repetir por primera vez su posición inicial.