MaterialFolleto 8ª OMM-MICH
1. ¿Para qué valor entero de n el número 2×10n está más cercano a [601.2/0.03]? 2. En un torneo de futbol hay 8 equipos. Cada equipo juega con cada uno de los demás exactamente una vez. ¿Cuántos partidos se juegan en todo el torneo? 3. Después de hacer un descuento de 20% una bicicleta cuesta N$1000. ¿Cuál es el precio original? 4. Si a y b son números positivos distintos que cumplen a2 + b2 = 4ab, hallar el valor de ([(a+b)/(a-b)])2. 5. En un triángulo ABC, P es un punto sobre el lado BC que lo divide en la razón 2:1, y Q es un punto sobre el lado AC que lo divide en la razón 3:1 (ver figura (a)). Suponiendo que el área del triángulo ABC es 18 cm2, ¿cuál es el área del triángulo APQ?
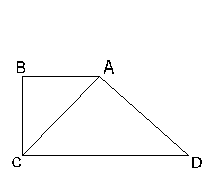
6. En la figura (b) los ángulos ABC y DAC son rectos, los segmentos AC y AD son iguales y los segmentos BC y BA son iguales y cada uno de estos dos mide 3cm. Calcular el área del cuadrilátero ABCD. 7. En un triángulo equilátero de papel se doblan las tres esquinas hacia adentro de tal manera que los tres vértices queden justo en el centro del triángulo. Describir el contorno de la figura obtenida. 8. La suma de los 1993 elementos de un cierto conjunto de números es 19931993. Hallar el promedio de los elementos de ese conjunto.
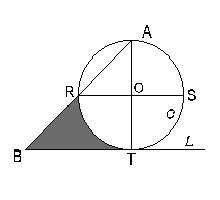
9. En la figura (c) (abajo) se muestra un dibujo con las siguientes condiciones: El círculo C tiene centro O y su diámetro mide 3. Los segmentos AT y RS son diámetros perpendiculares del círculo. La recta L es tangente al círculo en el punto T; B es la intersección de la recta L con la recta AR. Calcular el área de la región sombreada (delimitada por los segmentos BR y BT y el arco de círculo de R a T.)
10. Considera la sucesión de números a1, a2, a3, ¼ que está definida por:
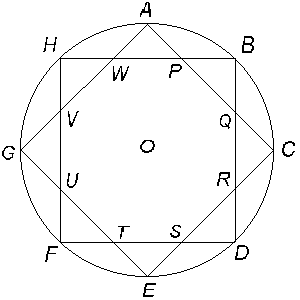
Calcula el producto a1×a2 ×a3×¼×a15 de los primeros 15 términos de la sucesión. [Escribe la respuesta en la forma [p/q] con p y q enteros.] 11. ¿Cuántos números enteros del 1 al 1993 (inclusive) al elevarlos a la vigésima potencia el resultado es un número terminado en 1? (En otras palabras, ¿para cuántos n la cifra de las unidades de n20 es 1?) 12. En la figura (d) (abajo) está dibujada una estrella con las siguientes características: El círculo tiene centro O y radio 1; los puntos A, B, C, D, E, F, G y H están sobre la circunferencia y forman un octágono regular; P es la intersección de la recta AC con la recta BH y los puntos Q, R, S, T, U, V y W están construidos de manera similar (como las intersecciones de las rectas respectivas como se ve en la figura). Hallar el área de la estrella.
13. Si c es un número entero positivo, llamemos P(c) al producto de las cifras de c (por ejemplo, P(414) = 16 y P(70) = 0). ¿Cuántos enteros positivos c menores que 100 000 satisfacen P(c) = 243? 14. En el plano se encuentran 10 conjuntos de rectas de manera que un conjunto tiene una recta, otro tiene dos rectas, otro tres y así sucesivamente hasta diez. Las rectas de cada uno de los diez conjuntos son paralelas entre sí pero no son paralelas a las de ninguno de demás conjuntos. Además entre todas las rectas no hay tres concurrentes (es decir, no hay tres rectas que pasen por un mismo punto). Calcula el número de puntos de intersección que tiene la colección completa de las rectas (cada dos rectas no paralelas determinan un punto de intersección). |
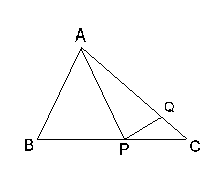 Figura (a)
Figura (a)