MaterialFolleto 9ª OMM-MICH
1. Una niña tiene tres listones (uno rojo, uno verde y uno blanco) que colocará en su pelo formando diademas. ¿Para cuántos días le alcanzan si quiere combinarlos de manera diferente cada día? (Cada día usará al menos uno y puede juntarlos para buscar distintas combinaciones sin importar el orden en que queden colocados.) 2. Decir cuál de los siguientes números es mayor que los demás:
3. La suma de cuatro números enteros consecutivos es 1994. ¿Cuál es el menor de esos cuatro números? 4. A una cantidad le sumo su 10%, y a la cantidad así obtenida le resto su 10%. ¿Qué porcentaje de la cantidad original me queda? 5. El producto de tres enteros mayores que 1 y distintos entre sí es 100. ¿Cuáles son los tres enteros? 6. En un rectángulo ABCD (ver figura (a)) M y N son los puntos medios de AD y BC, respectivamente, y P y Q son las respectivas intersecciones de AC con BM y con ND. Suponiendo que AD mide 5cm y que AB mide 3cm, ¿cuántos centímetros cuadrados tiene de superficie el cuadrilátero MPQD? 7. Un círculo cuyo radio mide 1cm está inscrito en un cuadrado y éste, a su vez, está inscrito en otro círculo (ver figura (b)). ¿Cuántos centímetros mide el radio de éste último círculo? 8. Se construyó un cubo de alambre de 3cm de lado y se marcaron divisiones con el mismo alambre para que en el cubo quedaran marcados 27 cubitos de 1cm de lado. ¿Cuántos centímetros de alambre se usaron (si no hubo desperdicio)?
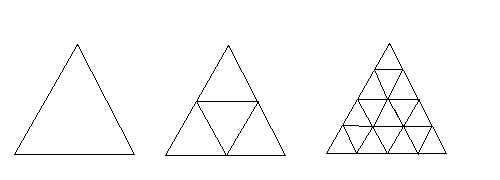
Los siguientes 6 problemas constituyeron el examen de la 1a Etapa del Concurso Michoacano de la 8a Olimpiada Mexicana de Matemáticas. Su duración fue de 3 h.9. Un cubo se encuentra inscrito en una esfera cuyo radio mide 1 cm. ¿Cuál es la longitud del lado del cubo? 10. En el piso se va a pintar un triángulo equilátero de 1 m de lado. Dentro de él se pintarán líneas paralelas a los lados partiendo de los puntos medios de los lados para formar triángulos equiláteros más chicos; los nuevos triángulos así obtenidos se dividirán siguiendo el mismo procedimiento y así sucesivamente (ver la figura). Se dispone de pintura para pintar hasta 200 m. ¿Cuál es la longitud de los triángulos más chicos que se pueden pintar? (Nota: Puede sobrar pintura pues se quiere que la figura que quede tenga todos los triángulos del mismo tamaño.)
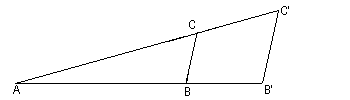
11. En un triángulo ABC se prolongan las rectas AB y AC hasta que corten una recta paralela a BC; a los puntos de intersección se les llama B¢ y C¢, respectivamente (ver la figura). Si el área de ABC es 1 y el área de AB¢C¢ es 2, ¿cuánto vale [AB/(BB¢)]?
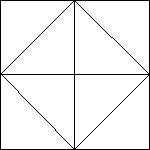
12. Encontrar el mayor número entero que no tenga cifras repetidas y tal que el producto de sus cifras sea el cuadrado de otro número entero distinto de cero. 13. Se quiere fabricar un juego de fichas cuadradas de cartón en las que una cara de la ficha sea negra y la otra esté pintada de colores con el diseño de triángulos que se muestra en la figura. Se usarán 4 colores (aunque no todas las fichas usen los 4). Se quiere que las fichas sean simétricas desde su centro y que dos triángulos adyacentes no tengan el mismo color (dos triángulos no adyacentes sí pueden llevar el mismo color). ¿Cuántas fichas deberá tener el juego si se quiere abarcar todas las posibilidades y que no haya fichas iguales? (Nota: Una ficha puede parecer distinta a otra al colocarse sobre la mesa pero si al girarse queda igual, sólo deberá tomarse en cuenta una de ellas.)
14. (Problema propuesto por Jorge Luis López López) En una balanza se utilizan pesas marcadas en gramos (cantidades enteras) para determinar el peso de objetos de la manera usual, es decir, colocando las pesas necesarias en cada lado de la balanza para que se equilibre.
|
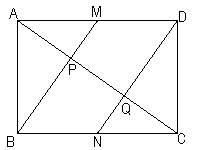 figura (a)
figura (a) 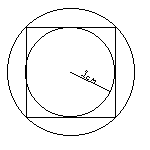 figura
(b)
figura
(b)