MATLAB

Input/Output files

To load data from a file: 
x=load('myfile.dat');   % load content of myfile.dat in an array x
To load data from different files: 
dir;              % display all files in the current directory (like ls)
f=dir;            % creates a structured array of "files" objects 
f=dir('*.dat');   % creates an structured array of data files objects 
f(1).name;        % return the name of the first file

for i=1:length(f);    % for each file 
  x=load(f(i).name);  % load each file i
  myfunction(x);      % do something with x
end

To save data in a file: 
save myfile var1 var2 ... -ASCII
or 
save('myfile', 'var1', 'var2',...,'-ASCII')
or (if you want to index your file) 
index=i;
myfile = sprintf('file%d.dat',index);
save(myfile, 'var1', 'var2',...,'-ASCII')
or (if you want to concatenate strings) 
fileext='dat';
myfile = sprintf('myfile.%s',fileext);
save(myfile, 'var1', 'var2',...,'-ASCII')

To write (formatted) text in a file: 
fID=fopen('mytextfile.txt','w'); % file ID ('w' means "open or create new file for Writing")

myformat='%s\t%g\n';             % my format

D1='The value of pi is:';        % string data
D2=3.14159;                      % numeric data

fprintf(fID,myformat,D1,D2);     % write in file

fclose(fID);                     % close file  				

type mytextfile.txt;             % display the content of the file

To save figures in a file: 
nfig=1; % number of the figure
set(nfig,'PaperPositionMode','auto'); % to keep aspect ratio when saving in file

saveas(gca,'myfigure.jpg','jpg');    % save current figure as jpg file
 or 
saveas(gca,'myfigure.eps','eps');    % save current figure as eps file

Random numbers

To initialize the randomizer: 
rand('state',sum(100*clock));
To generate...

one random value from a uniform distribution between 0 and 1: 
z=rand()
a 5x5 matrix of random values from a uniform distribution between 0 and 1: 
z=rand(5)
a vector of 5 random values from a uniform distribution between 0 and 1: 
z=rand(5,1)
a vector of 5 random values from a uniform distribution between 0 and 10: 
z=10.*rand(5,1)
a vector of 5 random integer values from a uniform distribution between 0 and 10: 
z=ceil(10.*rand(5,1))
a vector of 5 random values from a normal distribution of mean 0 and standard devation 1: 
z=randn(5,1)
a vector of N random values from a normal distribution of mean m and standard devation s: 
m=5;     % mean 
s=2;     % standard deviation
N=100;   % number of numbers to generate
z=m+s.*randn(1,N);
a random number from a binomial distribution with parameters specified by the number of trials, N, and probability of success for each trial, p: 
N=100;    % number of trials
p=0.7;    % probability of success
z=binornd(N,p);
a matrix of n x m random values from a binomial distribution (with N trials and probability p of success): 
N=10;    % number of trials
p=0.5;   % probability of success
n=5;
m=5;
z=binornd(N,p,[n,m])
a matrix n x m of random values with proba p to get a non-null value (i.e. a "sparse" random matrix): 
p=0.5;   % probability to have a non-nul value
n=5;
m=5;
z=rand(n,m).*binornd(1,p,[n,m])
a vector of N random values from a log-normal distribution of mean m and standard devation s: 
m=5;     % mean 
s=2;     % standard deviation
N=100;   % number of numbers to generate
mn=log(m^2/sqrt(s^2+m^2));
sn=sqrt(log(s^2/m^2+1));
z=exp(mn+sn.*randn(1,N));
a vector of N=100 numbers from a gamma distribution with mean m=5 and standard deviation s=5: 
m=5;        % mean
s=5;        % st dev
N=100;      % number of random numbers to generate
a=m/s ;     % shape parameter
b=m^2/s ;   % scale parameter
x=gamrnd(a,b,[1 N]);
a random permutation of the integers 1:n 
n=8;
z=randperm(n)
random permutation of the elements of a vector 
v=[2 4 6 8 10];
w=v(randperm(length(v)))

Solving equations

To solve equations symbolically 
eq1=sprintf('a-(b+1)*x+x^2*y');
eq2=sprintf('b*x-x^2*y');

sol=solve(eq1,eq2,'x','y');

sol.x
sol.y
To solve equations numerically 
a=2;
b=5.2;

eq1=sprintf('%d-(%d+1)*x+x^2*y',a,b);
eq2=sprintf('%d*x-x^2*y',b);

sol=solve(eq1,eq2,'x','y');

sol.x
sol.y
Selecting real solutions 
eq1=sprintf('2/(1+Y^4)-X=0');
eq2=sprintf('2/(1+X^4)-Y=0');

sol=solve(eq1,eq2,'X','Y');

sol.X
sol.Y

x=eval(sol.X)
y=eval(sol.Y)

k=find(imag(x)==0);

sol=[x(k) y(k)]

Fitting

Polynomial fit 
%%% Data

x=[0 1.6 2.6 4.1 5.1 6.5 7.4 8.9 9.6];
y=[-10.3 0.2 13.5 23 41.9 45.7 60.1 78.0 88.2];

%%% Correlation coefficient (if R close to 1, linear fit OK)

R=corrcoef(x,y);
R(1,2)

%%% Fitting

n=1;      % degree of the polynom (n=1 <=> linear fit)
p=polyfit(x,y,n)

%%% Write the function

fprintf('Best fit: y = %g x + %g nn',p(1),p(2))

%%% Figure

xfit=x;
yfit=p(1).*x +p(2);

plot(x,y,'bo',xfit,yfit,'r-');  

xlabel('x');
ylabel('y');
legend('data','fit',2)
Exponential fit 
%%% Data

t = [1:8] ; 
x = [629 537 460 375 334 286 249 227] ;

%%% Define your exponential function

fh = @(t,p) p(1) + p(2)*exp(-t./p(3))

%%% Error function (to be minimized)

errfh = @(p,x,y) sum((y(:)-fh(x(:),p)).^2)

%%% Initial guess of the exponential parameters

p0 = [mean(x) (max(x)-min(x)) (max(t) - min(t))/2];

%%% Search for solution

P = fminsearch(errfh,p0,[],t,x) 

%%% Write the function

fprintf('Best fit: x = %g + %g  exp(-t/%g) nn',P(1),P(2),P(3))

%%% Plot the result

tt=[1:0.1:8];
plot(t,x,'bo',tt,fh(tt,P),'r-')
xlabel('t')
ylabel('x')
legend('data','fit')

Figures

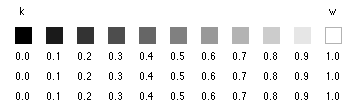
Time series plot
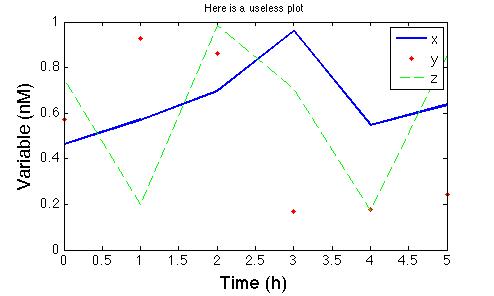  T=[0:5]    % this generates a vecteur T with number 0 to 5
  D=rand(6)  % this generates a 6x6 matrix with random number between 0 and 1
  figure(1)
  set(figure(1),'Position', [400 400 500 300]);  % size of the figure
  clf;   % to clean the figure
  plot(T,D(:,2),'b',T,D(:,3),'r.',T,D(:,4),'g--');
  xlabel('Time (h)','fontsize',18);
  ylabel('Variable (nM)','fontsize',18);
  xlim([0 5]);
  ylim([0 1]);
  title('Here is a useless plot')
  legend('x','y','z');
  set(gca,'xtick',[0:0.5:6],'fontsize',14);
  set(findobj(gca,'Type','line','color','blue'),'LineWidth',2);
Symbols plot
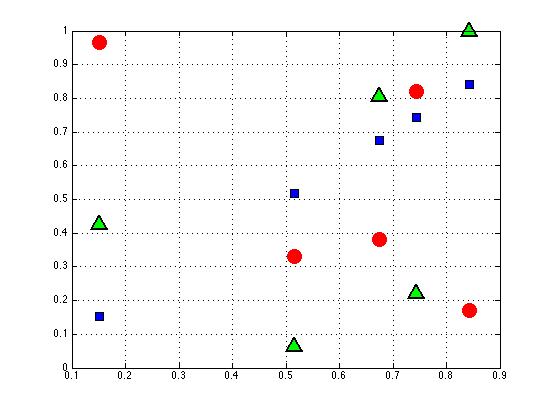  figure(3)
  clf;
  T=[1:5];
  X=rand(5,1);
  Y=rand(5,1);
  Z=rand(5,1);
  plot(X,X,'rs','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',10)
  hold on;
  plot(X,Y,'o','LineWidth',1,'MarkerEdgeColor','r','MarkerFaceColor','r','MarkerSize',15)
  hold on;
  plot(X,Z,'^','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',15)
  Y=rand(5,1)
  grid on;
Scatter plot
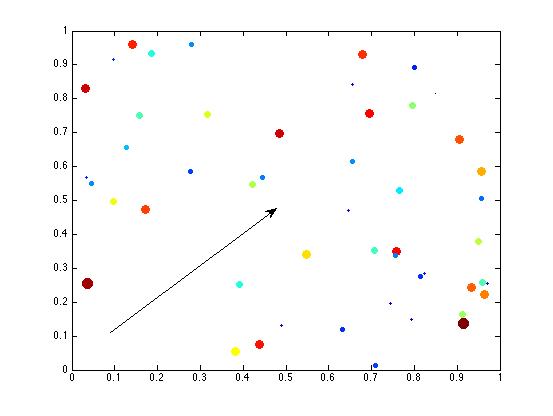  N=50;    % number of points to generate
  X=rand(1,N);   % x-position
  Y=rand(1,N);   % y-position
  Z=rand(1,N);   % value (color) of the points
  %s=50;            % size of the points (same for all points)
  %s=100*rand(1,N); % size of the points (random)
  s=100*Z;          % size of the points (same vector as color)
  figure(1)
  clf;
  scatter(X,Y,s,Z,'filled')
  annotation('arrow',[0.2 0.5],[0.2 0.5])   % draw arrow
  box on;
Error bar
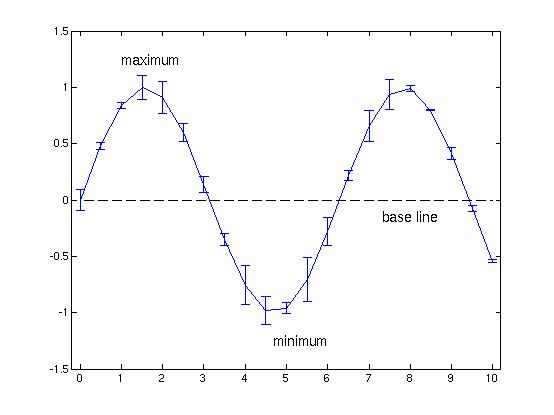    figure(1)
    clf;
    x=[0:0.5:10];
    y=sin(x);
    e=rand(1,length(x))/5
    errorbar(x,y,e)
    hold on;
    plot([0 10],[0 0],'k--')
    text(8,-0.15,'base line','fontsize',14,'HorizontalAlignment','center');
    text(1,1.25,'maximum','fontsize',14,'HorizontalAlignment','left');
    text(6,-1.25,'minimum','fontsize',14,'HorizontalAlignment','right');
    xlim([-0.2 10.2]);
    ylim([-1.5 1.5]);
    box on;
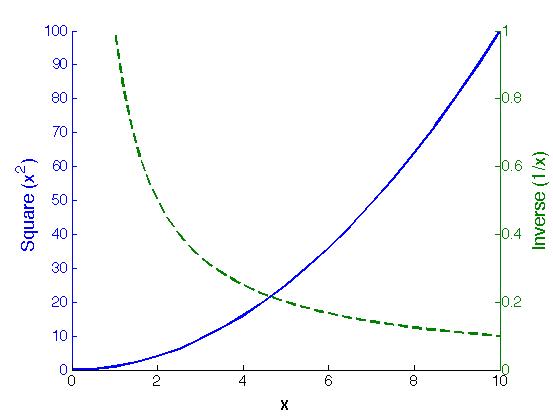
Double-y plot
    figure(1);
    clf;

    x1=[0:0.5:10];
    y1=x1.^2;
    x2=[0.2:0.2:20];
    y2=1./x2;

    [AX,H1,H2]=plotyy(x1,y1,x2,y2);

    box off;
    set(get(AX(1),'Ylabel'),'String','Square (x^2)','fontsize',18)
    set(get(AX(2),'Ylabel'),'String','Inverse (1/x)','fontsize',18)
    set(H1,'LineWidth',2)
    set(H2,'LineWidth',2,'LineStyle','--')
    xlabel('x','fontsize',18);
    set(AX(1),'YLim',[0 100],'YTick',[0:10:100],'fontsize',15)
    set(AX(2),'YLim',[0 1],'YTick',[0:0.2:1],'fontsize',15)
    set(AX(1),'xlim',[0 10]);
    set(AX(2),'xlim',[0 10]);
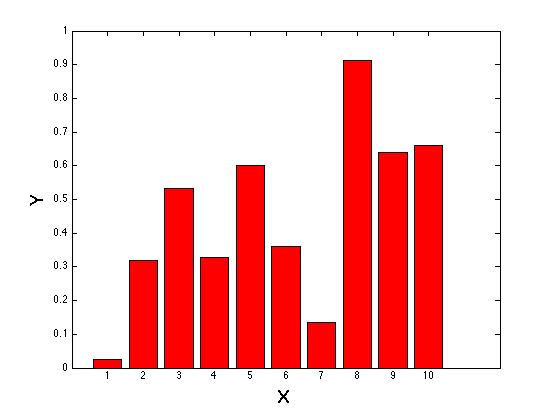
Bar plot
  figure(4)
  X=[1:10];
  Y=rand(10,1);
  bar(X,Y,'r');
  xlabel('X','fontsize',18);
  ylabel('Y','fontsize',18);
Bar plot (multicolor)
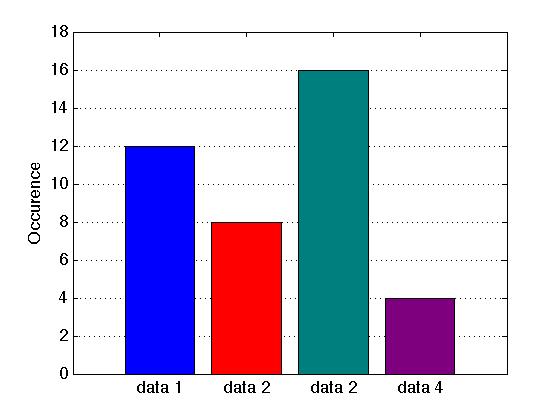  D=[12 8 16 4];  % data

  figure(1)
  b=bar(1:4,D);   %  bar plot

  %%% trick to personnalize the color of each bar:
  ch=get(b,'children');
  cd=repmat(1:numel(D),5,1);
  cd=[cd(:);nan];
  set(ch,'facevertexcdata',cd);
  colormap([[0,0,1];[1,0,0];[0,0.5,0.5];[0.5,0,0.5]]);

  set(gca,'YGrid','on')  % horizontal grid

  ylim([0 max(D)+2]);

  set(gca,'XTickLabel',{'data 1','data 2','data 2','data 4'},'fontsize',14)
  ylabel('Occurence')
Bar plot with error bars
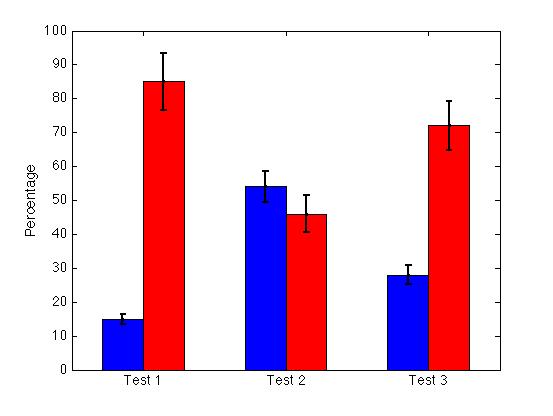figure(1)

clf;

D=[15 85; 54 46; 28 72];       % data
S=[1.5 8.5; 4.6 5.4; 2.8 7.2]; % st dev (10%)

h=bar(D);
set(h,'BarWidth',1);
hold on;

ngroups = size(D,1);
nbars = size(D,2);
groupwidth = min(0.8, nbars/(nbars+1.5));

colormap([0 0 1; 1 0 0]);   % blue / red

for i = 1:nbars
x = (1:ngroups) - groupwidth/2 + (2*i-1) * groupwidth / (2*nbars);
errorbar(x,D(:,i),S(:,i),'k.','linewidth',2);
end

set(gca,'XTickLabel',{'Test 1','Test 2','Test 3'},'fontsize',14)
ylabel('Percentage','fontsize',14)
Histogram
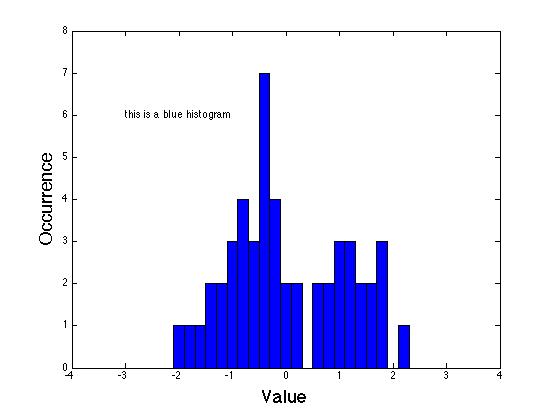  D=randn(50,1)  % generates a vector with 50 numbers normally distributed
  figure(2)
  bin=[-4:0.2:4];
  hist(D,bin);
  xlabel('Value','fontsize',18);
  ylabel('Occurrence','fontsize',18);
  xlim([-4 4]);
  ylim([0 8]);
  set(findobj(gca,'Type','patch'),'FaceColor','b','EdgeColor','k')
  text(-3,6,'this is a blue histogram')
Histogram with several populations
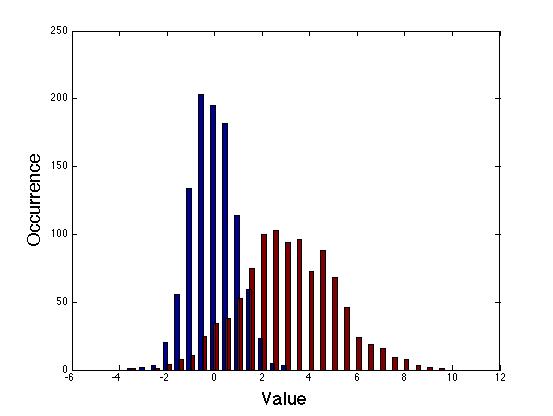  figure(2)
  D1=randn(1000,1);  % generates a vector with 1000 random numbers normally distributed
  D2=2*randn(1000,1)+3; % generates a vector with 1000 random numbers normally distributed
  x=[-5:0.5:10];
  y1=hist(D1,x);
  y2=hist(D2,x);
  D=[y1; y2];
  bar(x,D',1.4);
  xlabel('Value','fontsize',18);
  ylabel('Occurrence','fontsize',18);
Box plot
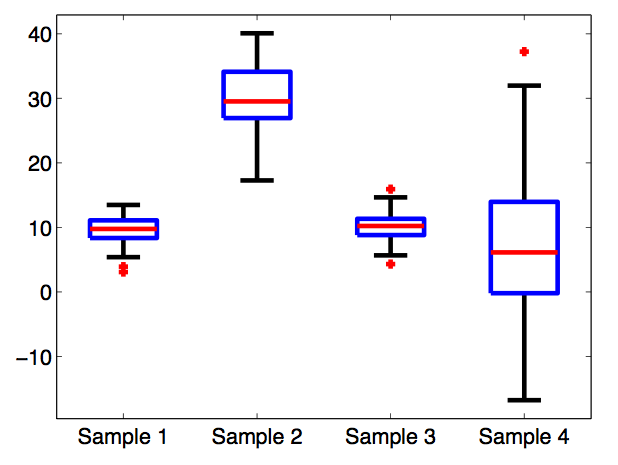n=100;  % number of data points / sample

D(1:n,1)=10+2*randn(1,n);  % sample 1
D(1:n,2)=30+5*randn(1,n); % sample 2
D(1:n,3)=10+2*randn(1,n);  % sample 3
D(1:n,4)=5+10*randn(1,n); % sample 4

figure(1)
clf

h=boxplot(D,'plotstyle','traditional','whisker',1.5);

%%% Some alternatives:
% 'plotstyle'= 'compact' => useful of many boxes
% 'whisker'= 1.5 (default) => increased not to display outliers 
% 'colors'='k' => plot in black

set(findobj(gcf,'LineStyle','--'),'LineStyle','-') % solid lines

for b=1:4 % loop on boxes
for i=1:size(h,1) % loop on the "elements" of a box
set(h(i,b),'linewidth',3);  % increase linewidth
end
end

mylabels={'Sample 1','Sample 2','Sample 3','Sample 4'};
mylabpos=[1:4];
set(gca,'XTickLabel',mylabels,'XTick',mylabpos,'fontsize',14);
Fill polygons
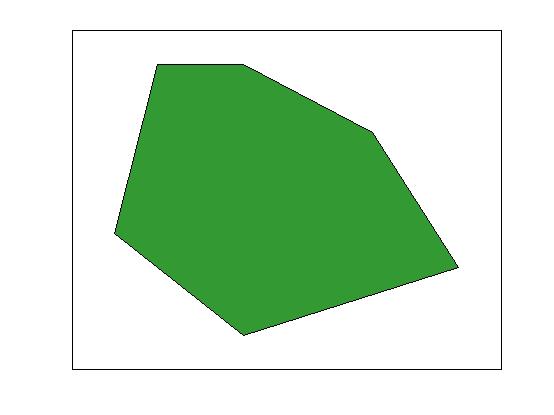  x = [1 2 4 7 9 4];
  y = [4 9 9 7 3 1];
  col=[0.2 0.6 0.2]; % colour (RGB)
  fill(x,y,col); 
  xlim([0 10]);
  ylim([0 10]);
  set(gca,'XTickLabel',{''})  % to remove x tick labels
  set(gca,'YTickLabel',{''})  % to remove y tick labels
  set(gca,'XTick',[])         % to remove x ticks
  set(gca,'YTick',[])         % to remove y ticks
  %axis off;                  % to remove the box
Color map
  X=rand(10);
  imagesc(X);
  colormap(jet);    % instead of 'jet' try 'gray', 'bone', 'spring',...
                    % >>help colormap for more color options.
  set(gca,'XTickLabel',{''})  % to remove x tick labels
  set(gca,'YTickLabel',{''})  % to remove y tick labels
  set(gca,'XTick',[])         % to remove x ticks
  set(gca,'YTick',[])         % to remove y ticks
Pie chart
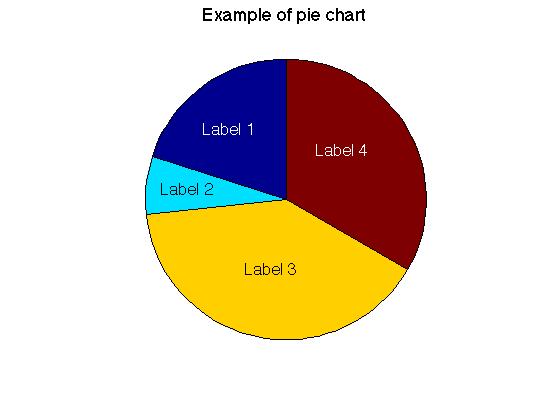  x=[30 10 60 50];
  explode = [0 0 0 0];
  %explode = [0 2 0 0];
  labels = {'Label 1', 'Label 2', 'Label 3', 'Label 4'};
  %labels = [];     % to indicate percents instead of labels

  h=pie(x,explode,labels);   % try pie3 for 3D pie...
                             % NB: if no labels, the percentage are indicated. 
			     
  %set(h(2:2:8),'fontsize',16); % sise of the labels
  set(h(2),'fontsize',16,'position',[-0.4 0.5],'color','w');   % label 1
  set(h(4),'fontsize',16,'position',[-0.7 0.07],'color','k');  % label 2
  set(h(6),'fontsize',16,'position',[-0.1 -0.5],'color','k');  % label 3
  set(h(8),'fontsize',16,'position',[0.4 0.35],'color','w');   % label 4

  colormap jet
  %set(h(1),'facecolor','m');   % change color of piece 1 into magenta

  title('Example of pie chart','fontsize',18)
  %set(gca,'position',[0.13 0.11 0.775 0.815])  % to change plot position 
  legend('lab1','lab2','lab3','lab4','location',[0.75 0.7 0.2 0.2])
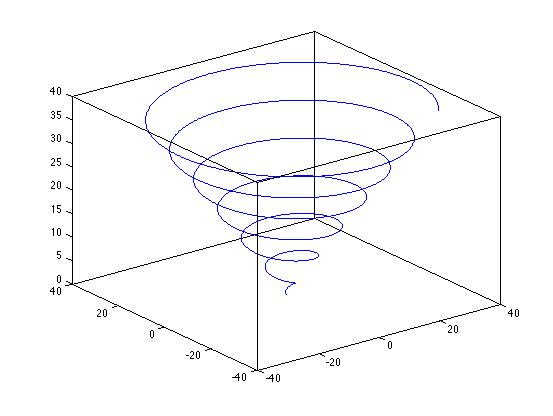
Plot 3D
  figure(8)
  clf;

  x=[0:0.01:40];

  plot3(x.*sin(x),x.*cos(x),x,'b')

  box on;
Surface
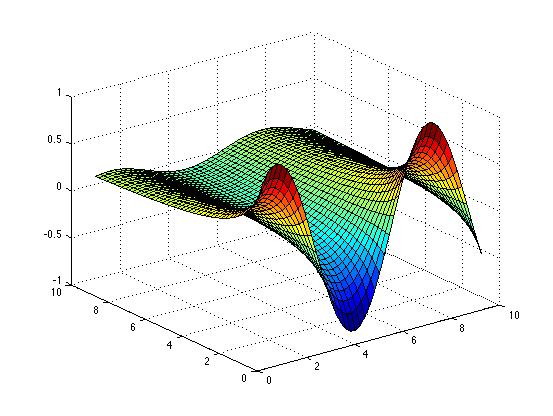  x=[1:0.2:10];
  y=[1:0.2:10];

  for i=1:length(x)
  for j=1:length(y)
    z(i,j)=1./x(i).*sin(y(j));
  end
  end

  figure(2);
  clf;
  surf(x,y,z);
Contour
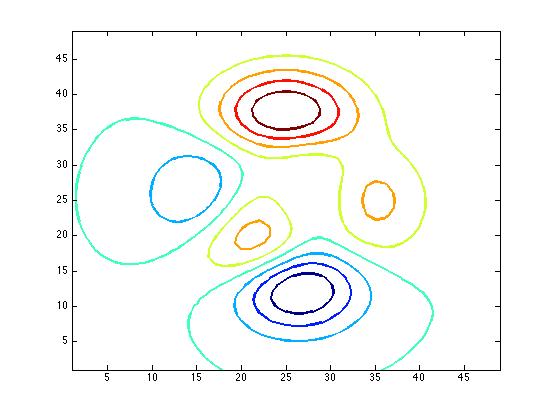  z=peaks;  % demo data
  
  figure(2)
  clf;
  n=8; % number of contour plot (not mandatory)
  contour(z,n,'linewidth',2);

  %%% To write level on the contour lines:
  % [C,h]=contour(z,n,'linewidth',2)
  % set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)

  %%% Alternative representations:
  % contourf(z,n)   % to fill the regions between the contours
  % contour3(z,n)   % to draw the contours in 3D
Surface + contour
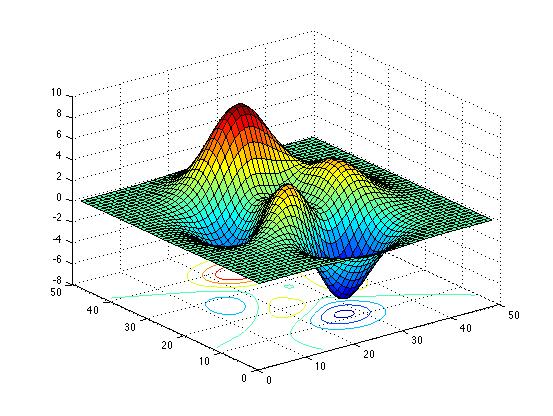  z=peaks;  % demo data

  figure(4)
  clf;
  h=surfc(z);
  clev=-8;   % z-level of the contour lines
  for n=2:numel(h)
     z=get(h(n),'zdata');
     set(h(n),'zdata',ones(size(z))*clev); % Contours are draw at z=clev
  end
Density
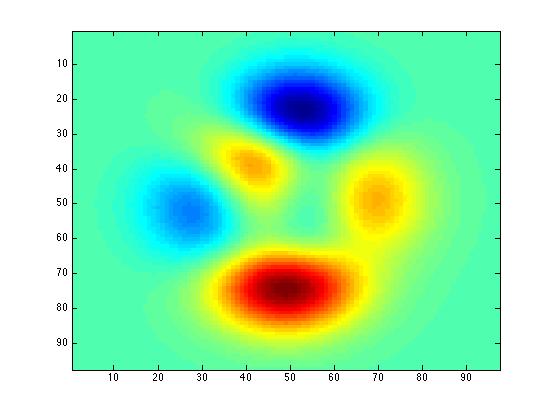  z=peaks;  % demo data
  
  figure(3)
  clf;
  niter=1;
  method='bilinear';
  y=interp2(z,niter,method);
  imagesc(y);
Geometrical shapes
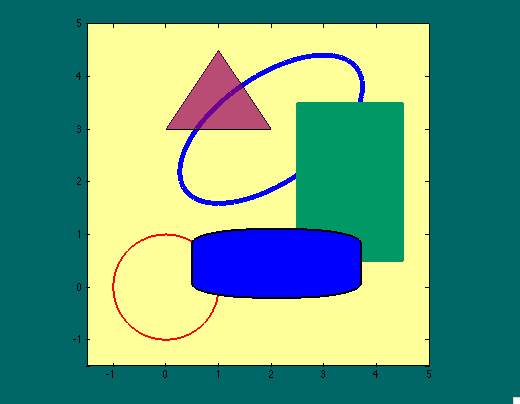  %%% background colors

  whitebg([1.0 1.0 0.6])         % background color (in+out plot)
  set(gcf,'Color',[0,0.4,0.4])    % background color (out plot only)

  %%% circle

  circle = rsmak('circle');
  fnplt(circle)
  set(findobj(gca,'Color','blue'),'Color','r','LineWidth',2)

  xlim([-1.5 5])
  ylim([-1.5 5])
  axis square

  %%% ellipse

  hold on;
  S=[2,1];                                    % stretch
  T=[2;3];                                    % translation
  a=35*2*pi/360;                              % rotation angle
  R=[cos(a) sin(a);sin(a) -cos(a)];           % rotation matrix
  ellipse = fncmb(circle,[S(1) 0;0 S(2)]);    % stretch
  rtellipse = fncmb(fncmb(ellipse, R), T );   % rotate
  fnplt(rtellipse)
  set(findobj(gca,'Color','blue'),'Color','b','LineWidth',4)

  %%% rectangle
  
  hold on;
  c=[0.0 0.6 0.4];
  rectangle('Position',[2.5,0.5,2,3],'LineWidth',2,'facecolor',c,'edgecolor',c)

  %%% rounded rectangle

  hold on;
  rectangle('Position',[0.5,-0.2,3.2,1.3],'Curvature',[0.8,0.4],'LineWidth',2,'facecolor','b')

  %%% triangle

  hold on;
  h=patch([0 1 2], [3 4.5 3],'g');
  set(h,'facecolor',[0.6 0.0 0.4],'facealpha',0.7)
Voronoi plot
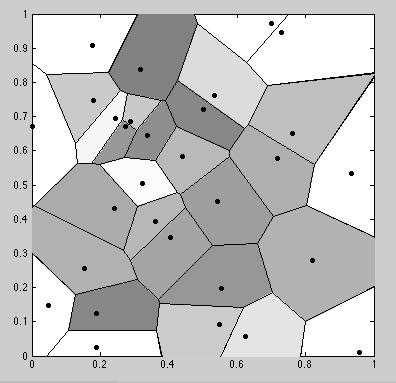  N=30;  % number of cells

  x=rand(1,N);
  y=rand(1,N);

  D=[x;y]';

  [v,c]=voronoin(D);  % get edges

  for p=1:N

  r=rand()/2+0.5;    % color: random light grey 
  col=[r r r];

  patch(v(c{p},1),v(c{p},2),col);  % color
  hold on;
  plot(x(p),y(p),'k.')        % dot at "center"

  end

  voronoi(x,y,'k')   % plot edges

  axis equal
  box on
  xlim([0 1])
  ylim([0 1])
Sphere
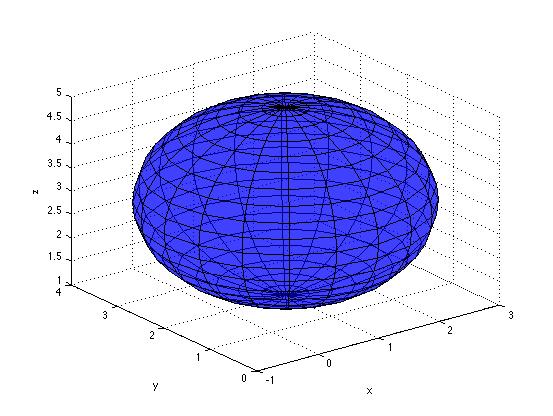  r=20;               % resolution
  a=2;                % size of the sphere
  xc=1;yc=2;zc=3;     % coordinates of the center
  alpha=0.5;          % transparency 

  [x,y,z]=sphere(r);

  figure(1)
  clf;

  surf(xc+x*a,yc+y*a,zc+z*a,'facecolor','blue','edgecolor','k','facealpha',alpha)
  %colormap('jet')   % colormap can be used if facecolor not used 

  xlabel('x');
  ylabel('y');
  zlabel('z');
Cube
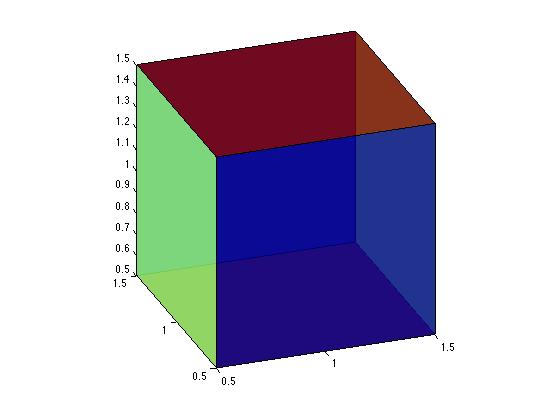xc=1; yc=1; zc=1;    % coordinated of the center
L=1;                 % cube size (length of an edge)
alpha=0.8;           % transparency (max=1=opaque)

X = [0 0 0 0 0 1; 1 0 1 1 1 1; 1 0 1 1 1 1; 0 0 0 0 0 1];
Y = [0 0 0 0 1 0; 0 1 0 0 1 1; 0 1 1 1 1 1; 0 0 1 1 1 0];
Z = [0 0 1 0 0 0; 0 0 1 0 0 0; 1 1 1 0 1 1; 1 1 1 0 1 1];

% C='blue';                                                   % unicolor
C= [0.1 0.5 0.9 0.9 0.1 0.5];                                 % color/face
% C = [0.1 0.8 1.1 1.1 0.1 0.8 ; 0.2 0.9 1.2 1.2 0.2 0.8 ;  
%      0.3 0.9 1.3 1.3 0.3 0.9 ; 0.4 0.9 1.4 1.4 0.4 0.9 ];   % color scale/face

X = L*(X-0.5) + xc;
Y = L*(Y-0.5) + yc;
Z = L*(Z-0.5) + zc; 

fill3(X,Y,Z,C,'FaceAlpha',alpha);    % draw cube
axis equal;

AZ=-20;         % azimuth
EL=25;          % elevation
view(AZ,EL);    % orientation of the axes
Multi-plot
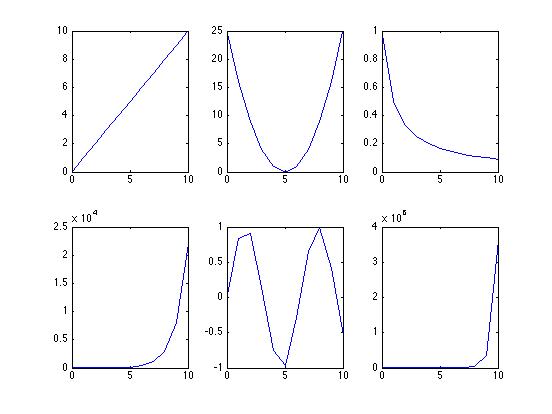  figure(1)
  clf;
  
  x=[0:10];

  subplot(2,3,1)
  plot(x,x)
  
  subplot(2,3,2)
  plot(x,(x-5).^2)

  subplot(2,3,3)
  plot(x,1./(x+1))

  subplot(2,3,4)
  plot(x,exp(x))

  subplot(2,3,5)
  plot(x,sin(x))

  subplot(2,3,6)
  plot(x,factorial(x))
Multi-plot
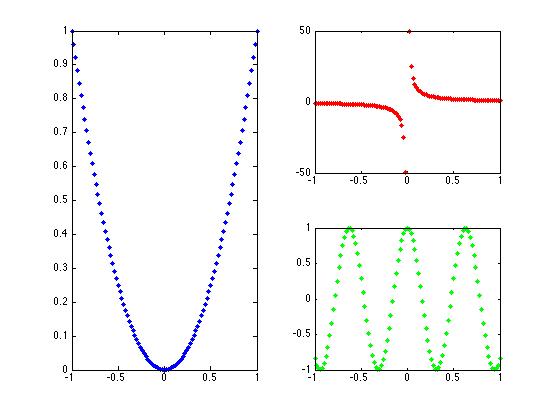  figure(1)
  clf;
  
  x=[-1:0.02:1];

  subplot(2,2,[1 3])
  plot(x,x.^2,'b.')

  subplot(2,2,2)
  plot(x,1./x,'r.')

  subplot(2,2,4)
  plot(x,cos(10.*x),'g.')
Multi-plot
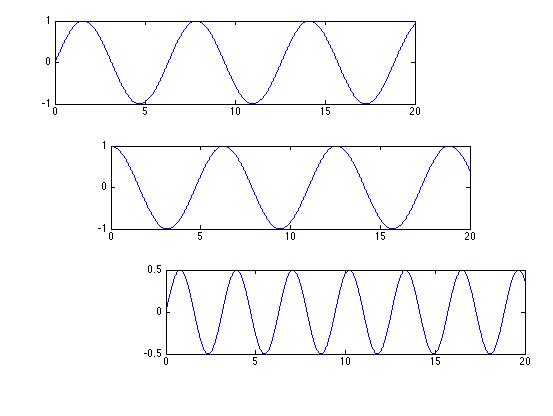  figure(1)
  clf;

  x=[0:0.01:20];

  subplot('Position',[0.1 0.75 0.65 0.2])
  plot(x,sin(x),'b')

  subplot('Position',[0.2 0.45 0.65 0.2])
  plot(x,cos(x),'b')

  subplot('Position',[0.3 0.15 0.65 0.2])
  plot(x,sin(x).*cos(x),'b')
Inset
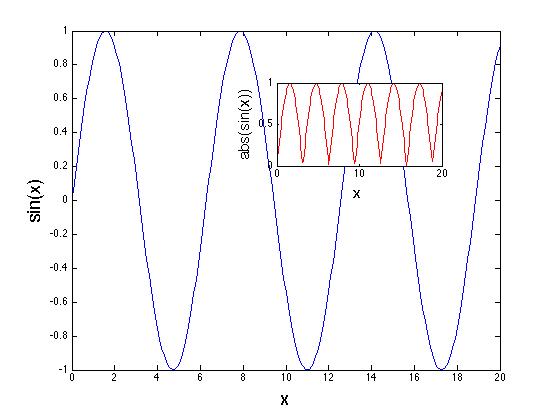  figure(1)
  clf;

  x=[0:0.1:20]
  y=sin(x)

  subplot(1,1,1) ; % main plot

  plot(x,y,'b')
  xlabel('x','fontsize',18)
  ylabel('sin(x)','fontsize',18)

  axes('position',[0.5 0.6 0.3 0.2]) ; % inset

  plot(x,abs(y),'r')
  xlabel('x','fontsize',15)
  ylabel('abs(sin(x))','fontsize',15)

Color code

Colors can be defined by a vector of 3 elements (RGB code): 
color=[r g b];  % r=red, g=green, b=blue
Some colors can also be referred to by their "name". Examples: 
color='b';   % blue
color='k';   % black
color='m';   % magenta
Here is the code (r,g,b) and the name for different colors.

Color scale



Grey scale



Here are some demo programs

Simulation
Simulating a discrete iterative system
(logistic equation)		25/1/2008logistic.m
Simulating a 2-ODE system
(Bruxellator)		29/1/2008brusselator.m
Simulating a 2-ODE system + plot the direction field
(Toggle switch)		31/1/2009togglequiver.m
Simulating a 2-ODE phase oscillator
(limit-cycle phase oscillator)		14/7/2008phaseoscillator.m
Simulating a 3-ODE system
(FRQ model for circadian clock)		25/1/2008frq.m
Simulating a 3-ODE system + sensitivity analysis
(FRQ model for circadian clock)		19/12/2012frqsensitivity.m
Simulating a forced 3-ODE system
(FRQ model for circadian clock entrained by a LD cycle)		29/1/2008frqforced.m
Simulating a perturbed 3-ODE system + phase response curve
(FRQ model for circadian clock perturbed by a light pulse)		22/7/2008frqprc.m
Simulating a 3-ODE system with a conditional resetting of a variable
(Ruoff model)		13/8/2009ruoff.m
Simulating a chaotic 3-ODE system
(Rossler model)		8/7/2008rossler.m
Simulating a 2-variable DDE system
(Delay differential models for circadian clock:
Scheper model with 1 delay + Sriram model with 3 delays)		16/7/2008delaymodel1.m
delaymodel2.m
Simulating a system of coupled oscillators (N x 4-ODE system)
(Coupled Goodwin oscillators via (1) a mean field or (2) a coupling matrix)		29/5/2008goodwinsynchro1.m
goodwinsynchro2.m
Simulating a system with diffusion
(1D and 2D simple Fick model)		24/5/2008
29/5/2008		fick.m
fick2D.m
Simulating a reaction-diffusion system
(Reaction-diffusion Brusselator - 2D)		29/5/2008bruxRD2D.m
Simulating a reaction-diffusion system
(Propagating front)		8/9/2012RDfront.m
Simulating a stochastic system with the Gillespie algorithm
(Stochastic FRQ model)		13/7/2007frqstocha.m
Simulating a stochastic system with the Langevin algorithm
(Stochastic Brusselator model)		26/1/2007bruxLange.m
Time series analysis (deterministic time series)
Maxima (all maxima of a time series)28/10/2014maxima.m
Minima (all minima of a time series)28/10/2014minima.m
Period (for deterministic oscillations)2/1/2011period.m
Amplitude (for deterministic oscillations)2/1/2011amplitude.m
Phase (for deterministic oscillations)2/1/2011phase.m
Damping (for deterministic oscillations)2/1/2011damping.m
Poincare section8/3/2011poincare.m
Order parameter (for synchronized oscillations)19/10/2010orderparam.m
Time series analysis (stochastic time series)
Auto-correlation function
(for stochastic oscillations)		30/1/2008autocorrelation.m
Period distribution - naive approach
(for stochastic oscillations)		30/1/2008distriper.m
Period distribution using Hilbert transform
(for stochastic oscillations)		12/12/2009hilbertperiod.m
Fourier transform
(for stochastic oscillations)		9/7/2008myfft.m
Data analysis and statistics
Coefficient of determination (R-squared)14/4/2014rsq.m
Bray-Curtis distance3/8/2013braycurtis.m
Hurst exponent15/4/2014hurst.m
Data visualisation
Actogram (ex: actogram.png)21/10/2010actogram.m
Raster plot (ex: raster.png)29/12/2010raster.m
Graph (as in Graph theory) (ex: graph.png, graph2.png)4/8/2013graph.m
graph2.m
Plot matrix (with color scale) (ex: plotmatrix.png)30/7/2014plotmatrix.m
Time series profile (ex: tsprofile.png)8/5/2014tsprofile.m
Plot color points (from a data matrix) (ex: plotcolorpoints.png)21/10/2015plotcolorpoints.m
Phase circle (ex: phasecircle.png)18/11/2015phasecircle.m
Simplex (ternary) plot (ex: simplex.png)10/12/2015simplex.m
Cellular automaton
Wolfram's automata (1D)
(see some results here)		27/7/2008wolfram.m
Game of Life (2D)
(see some results here)		27/7/2008gameoflife.m
Cell cycle automaton
(see scheme of the model here and results here)		6/11/2008
16/11/2008		cdcautomaton.m
cdcautoanim.m
Hubbell model (population dynamics)
+spatial extension		24/7/2012hubbell.m
hubbell_spatial.m
Other automata
(Langton's ant, Diffusion, Aggregation, Sand pile, etc)		28/12/2010See here
Random walks
Random walk
30/12/2008randomwalk.m
Brownian movement
30/12/2008brownian.m
Fibonacci and Golden ratio
Fibonacci numbers
31/12/2008fibonacci.m
Golden spiral
31/12/2008goldspiral.m
Golden plant
31/12/2008goldplant.m
Golden tree
31/12/2008goldtree.m
Tournesol
31/12/2008tournesol.m
Chaos and Fractals
Fractals: Cantor, Koch, Sierpinsky, Menger, Julia, Mandelbrot,...25/1/2008See here
Henon map21/11/2012henon.m
Baker's transform23/12/2012baker.m
Miscellaneous
Arrow (add arrow(s) on a plot)30/4/2015arrows.m
Circle2/8/2013circle.m
Moebius strip26/12/2011moebius.m
Perimeter of polygones3/11/2013polyperim.m
Intersection12/12/2013intersection.m
Voronoi neighbours (get neighbours in a Voronoi diagram)2/11/2013voroneighbours.m
Scale-free network25/4/2014SFnet.m
Image manipulation
Image deformations
(applied here to clownfish1.jpg)		21/7/2008imtransfo.m
Image colors changes
(applied here to clownfish1.jpg)		21/7/2008imcolor.m
Image superposition
(applied here to clownfish1.jpg and clownfish2.jpg)		21/7/2008imsuper.m
Photomaton
(applied here to monalisa_256.jpg => monalisa_out.jpg)		24/7/2010photomaton.m
Transformation du Boulanger
(applied here to monalisa_256.jpg => monalisaboul.png)		9/10/2011boulanger.m
Photocube
(applied here to photo1.jpg+photo2.jpg+photo3.jpg => photocube.jpg)		17/8/2012photocube.m
Animation
Rotating cube
(see animation here)		3/1/2009rotatingcube.m
Lighted sphere
(see animation here)		15/2/2009lightsphere.m
Transparent icosahedron
(see animation here)		15/2/2009icosahedron.m


Didier Gonze - Created: 25/1/2008 - Updated: 15/12/2015 - [back] - [home]