Heurísticas
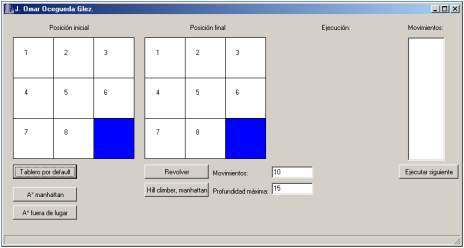
Programa de ejemplo    Las funciones "de decisión" llamadas heurísticas se utilizan como un medio para acelerar las búsquedas tradicionales. Podemos definir sin mucho formalismo una heurística como una función que asigna a cada posición A de nuestra búsqueda, otra posición B tal que B es "alcanzable" desde A. La noción de "alcanzable" depende del contexto en el que nos encontremos, en este caso particular, una configuración del tablero B es alcanzable desde otra configuración A si arrastrando algún cuadrito del tablero A nos queda la configuración del tablero B.

   Muy a menudo la heurística se basa en otra función llamada "función de costo", que es simplemente una función que asigna a cada posición de nuestra búsqueda un número no necesariamente entero, que puede verse como una especie de medida de distancia entre la posición actual de la búsqueda y la solución que deseamos.

   Claramente en general es difícil saber con precisión esta medida, por lo que la función de costo es simplemente una estimación de la medida de distancia real. Se dice que una función de costo es consistente si subestima la función de medida exacta.

   Dada una función de costo C(X) podemos definir la heurística de nuestro problema como H(X)=Y donde Y es tal que minimiza la función de costo C(Y) sobre el conjunto de posiciones alcanzables desde X.

   Entre las funciones de costo más populares está la medida de "manhattan". El algoritmo A* utiliza una heurística basada en una función de costo que no solamente depende de la posición actual de la búsqueda sino también de la "cantidad de trabajo" que tuvimos que realizar para llegar desde la posición inicial a la posición actual. Esta característica permite que A* encuentre soluciones razonablemente sencillas y en un tiempo computacional relativamente corto.

   Otro ejemplo de búsqueda guiada mediante una función de costo es el conocido como "hill climber", que es una búsqueda exhaustiva donde los nodos adyacentes se visitan tomando en cuenta un orden, definido por la función de costo, i.e. las posiciones alcanzables con menor función de costo se visitan primero.