Tarea 23 a)Reconstrucción de segmentos usando filtros de Gabor adaptables. (Colocando las franjas en dirección ortogonal a las gaussianas)

La idea original de este método era utilizar "filtros de Gabor alargados" orientados en varias direcciones de tal forma que las franjas quedaran orientadas en la misma dirección de la gaussiana base.

Sin embargo, pensé que sería mejor colocar las franjas en posición ortogonal a la dirección de la gaussiana base, de esta forma lo que obtenemos es un "detector de oyos" con una cierta frecuencia exclusiva.

Haciendo las cosas cuidadosamente, obtendremos una respuesta muy alta en los lugares de la imagen donde, localmente, las irregularidades tengan aproximadamente una cierta frecuencia. La idea es utilizar frecuencias suficientemente altas para detectar irregularidades pequeñas. Sin embargo, una "linea de división" está formada tanto por regiones irregulares (con ruido o algo) como por regiones regulares (donde la linea no sufrió daños) Entonces un paso adicional de este algoritmo es sumar a la imagen resultante la imagen original (de hecho es aplicar un "or") sobre ambas imágenes.

En seguida muestro el desarrollo de este algoritmo:

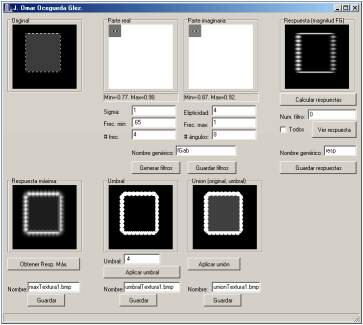
Parámetros	Imagen original	Máximo	Con umbral
Sigma=1 Elipticidad=3 Frecuencia=3.1 Num. filtros=10 Umbral=0.85

Utilizando una frecuencia cercana a PI, detectamos los "oyos pequeños", y con un umbral adecuado dejamos a un lado el resto de las lineas, que en realidad no nos interesan por ahora. Es interesante notar lo bien definida que queda la linea, es decir que el filtro no introduce irregularidades ni mucho suavisamiento como lo hace el filtro gaussiano adaptable.

Parámetros	Imagen original	Máximo	Con umbral
Sigma=1 Elipticidad=3 Frecuencia=1.5 Num. filtros=10 Umbral=0.85

Era de esperarse que fuera difícil encontrar una frecuencia adecuada de tal modo que tengamos respuesta alta únicamente en la linea que queremos... sin embargo la única linea continua es la segunda, ésto es en realidad lo que estamos tratando de lograr, que cada linea quede continua por si sola al filtrar con "su frecuencia"...

Parámetros	Imagen original	Máximo	Con umbral
Sigma=1 Elipticidad=3 Frecuencia=1 Num. filtros=10 Umbral=0.85

Parámetros	Imagen original	Máximo	Con umbral
Sigma=1 Elipticidad=4 Frecuencia=.8 Num. filtros=10 Umbral=0.85

No hay que dejarnos llevar por el buen resultado, le atinamos a la frecuencia "por pura chiripa", de hecho en una imagen mas general, no vamos a tener una frecuencia muy bien definida...

Parámetros	Imagen original	Máximo	Con umbral
Sigma=1 Elipticidad=4 Frecuencia=.65 Num. filtros=10 Umbral=0.85

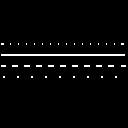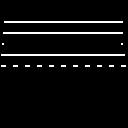
Bueno, bueno, si ya observamos que podemos obtener la respuesta deseada utilizando una cierta frecuencia, lo primero que se le ocurre a uno es decirle a la computadora que aplique el proceso utilizando todo un conjunto de frecuencias y que tome las respuestas mas altas... Entonces si elegimos M ángulos entre [0,PI], ya no solamente vamos a tener un banco de M filtros de Gabor, ahora tenemos que elegir un rango para las frecuencias [frecMin, frecMax], una cantidad de frecuencias F(la partición del intervalo de frecuencias) y alguna manera de distribuir las frecuencias. La manera más sencilla es elaborar una partición uniforme de [frecMin, frecMax]. Nuestro banco de filtros de Gabor aumenta a MxF.

Parámetros	Imagen original	Máximo	Con umbral
Sigma=1 Elipticidad=4 Frecuencia=0.65 a 2 Num. ángulos=10 Num. frecuencias=5 Umbral=0.85

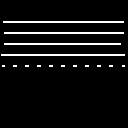
Claramente, si usamos una cantidad muy pequeña de frecuencias es muy difícil atinarle a la frecuencia buena para cada patrón de irregularidades (en este caso no encontramos el filtro adecuado para la cuarta linea), hay que aumentar la cantidad de frecuencias.

Parámetros	Imagen original	Máximo	Con umbral
Sigma=1 Elipticidad=4 Frecuencia=0.65 a 2 Num. ángulos=10 Num. frecuencias=8 Umbral=0.85

Ahora sí encontramos las cuatro franjas (nótese que frecMin=0.65 y frecMax=2, por eso no encontramos la primera linea, la cual requiere de un filtro con frecuencia muy cercana a PI). El último paso es agregarle la imagen original a la imagen resultante y así obtenemos el resultado que estábamos buscando.

Ésta es la imagen final:

Conclusiones: Puedo concluir mencionando las ventajas y desventajas que noté en este método:

Ventajas:

Es fácil notar que las lineas están muy bien definidas y no presentan las irregularidades que introduce el método de los kérneles gaussianos adaptables.
Ahora tenemos un método que podría restaurar lineas de tal forma que el usuario puede especificar los rangos en los que un "oyo" se considera una irregularidad, incluso es posible dejar pasar oyos pequeños y restaurar otros un poco mas grandes, cosa que no es posible con el método anterior.

El hecho de que este método NO restaure oyos excesivamente pequeños permite restaurar lineas que definen superficies con textura. Un kérnel gaussiano destruiría las texturas inmediatamente!!:

Método	Imagen rellena con textura	Respuesta máxima a los filtros	Reconstrucción del borde mediante umbral	Operador "or" con la imagen original
Gabor
Gaussiano

Desventajas:

Evidentemente el costo computacional es altísimo... se requieren dos convoluciones por cada filtro y obtener la norma da cada señal compleja...además de que la construcción de los filtros de Gabor direccionales es más costosa que los kérneles gaussianos direccionales.

Usando convolución normalizada podríamos evitar perder las lineas en las orillas, pero si ya de por si el método es lento, ésto lo haría aún más...

a)Reconstrucción de segmentos usando filtros de Gabor adaptables.
(Ahora con las franjas en dirección del eje principal de la gaussiana)

Método	Imagen rellena con textura	Respuesta máxima a los filtros	Reconstrucción del borde mediante umbral
Gabor(ortogonal a la gaussiana)
En dirección de la gaussiana Frecuencia=0.8*Pi Num. filtros=11

Con este ejemlo vemos una deficiencia del filtro de gabor con las franjas en dirección de la gaussiana, tiene muchos problemas en las esquinas; el filtro con las franjas en dirección ortogonal a la dirección principal de la gaussiana no tiene este problema.

La ventaja de este último método es que tiene una frecuencia fija que define el grosor de las lineas que deseamos preservar. Entonces el problema se aclara, lo que sucede es que las lineas que definen el contorno del rectángulo son del mismo grosor que las lineas punteadas que forman la textura de adentro. Es por eso que le cuesta trabajo diferenciarlas.

b) Modelo de Placas.
Optimización mediante descenso newtoniano.
A continuación muestro algunos ejemplos de aplicar el modelo de placas para tratar de eliminar el ruido de algunas imágenes.

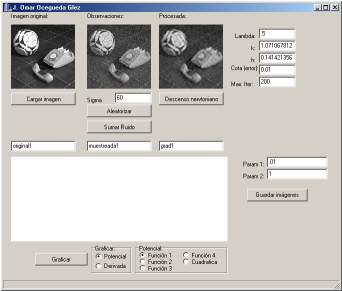
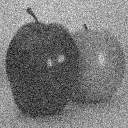
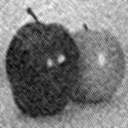
Imagen original	Con ruido Gaussiano	Aplicando modelo de resortes	Aplicando modelo de placas

Bueno, en realidad este modelo no funciona tan bien como los potenciales robustos, la mejora es que no suaviza tanto los bordes como el modelo de resortes con potencial cuadrático.