Ejercicios. Página 51.
1) Escriba una función para realizar convolución separable con 2 kerneles
arbitrarios h1, h2, usando las funciones ConvR y ConvC de la biblioteca
proc2D que realizan convoluciones con un renglón y una columna de una
imagen, respectivamente.
Las funciones ConvR y ConvC están definidas para imágenes de tamaño impar,
mejor redefiní las funciones. La generalización para imágenes a color
es, muy natural...
Imagen original y kernel


| Convolución por filas |
Convolución por columnas |
Convolución completa |
 |
 |
 |
La función "convolucionSeparable" aplica dos veces la convolución no circular para
el caso particular de una imagen de tamaño (1,n), y otra de (m,1).
//Realiza convolucion separable con los kerneles K1 y K2, aplicada al canal c
CimagenColor& CimagenColor::convolucionSeparable(CimagenColor& K1, CimagenColor& K2, int c)
{
CimagenColor *aux=new CimagenColor(largo, alto);
*aux=convolucionNoCircular(K1, c);
*aux=aux->convolucionNoCircular(K2, c);
return *aux;
}
Bueno, el código de la función de convolución no circular generalizada es el
siguiente:
CimagenColor& CimagenColor::convolucionNoCircular(CimagenColor& IC, int c)
{
CimagenColor *aux=new CimagenColor(largo, alto);
int centroFil=IC.alto/2, centroCol=IC.largo/2;//la ubicacion del impulso para dar la respuesta IC
int modFil=IC.alto%2;
int modCol=IC.largo%2;
double **gk=IC.canal[c];//señal auxiliar, kernel
for (int i=0;i<alto;i++)
gk[i]+=centroCol;
gk+=centroFil;
for (int i=0;i<alto;i++)
{
int k0=i-centroFil+1-modFil;//si modFil=1, entonces hay un pixel mas en la parte de arriba
if(k0<0)
k0=0;
int k1=i+centroFil;
if(k1 > (alto-1))
k1=alto-1;
for (int j=0;j<largo;j++)
{
int L0=j-centroCol+1-modCol;
if(L0<0)
L0=0;
int L1=j+centroCol;
if(L1>(largo-1))
L1=largo-1;
double suma=0;
for (int k=k0;k<=k1;k++)
for(int L=L0;L<=L1;L++)
suma+=canal[c][k][L]*gk[i-k][j-L];
aux->canal[c][i][j]=suma;
if(suma<aux->min[c])
aux->min[c]=suma;
if(aux->max[c]<suma)
aux->max[c]=suma;
}
}
gk-=centroFil;
for (int i=0;i<alto;i++)
gk[i]-=centroCol;
for (int k=0;k<3;k++)
if (k!=c)
{
for (int i=0;i<alto;i++)
for (int j=0;j<largo;j++)
aux->canal[k][i][j]=canal[k][i][j];
aux->min[k]=min[k];
aux->max[k]=max[k];
}
return *aux;
}
Ejercicios. Página 52.
1) Calcule el ahorro computacional (en %) al usar convolución separable para
un kernel Gaussiano de varianza 10 que se trunca para |x| > 3s
En este caso s=sqrt(10), aproximadamente igual a 3. entonces el kernel solo es distinto de cero en [-9,9]
entonces la longitud del kernel es n=19. Por lo tanto el ahorro es aproximadamente 90%. (2/19=0.10...)
Ejercicios. Página 53.
1) Grafique ejemplos de kerneles Gaussiano, de caja y binomial en 2D para
distintos valores de sus parámetros. Aplíquelos a una imagen a la que se la
haya añadido ruido y grafique tanto las imágenes suavizadas, como un renglón
específico de cada una de ellas. Comente sobre las diferencias de
comportamiento.
Imagen original y con ruido gaussiano

 Kérnel gaussiano
Kérnel gaussiano
| * |
Kérnel |
Convolución |
Renglón 64 (antes de convolución) |
Renglón 64 (después de convolución) |
| Varianza 25 |
 |
 |
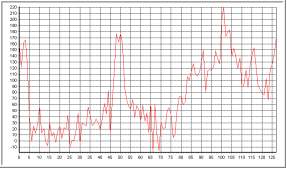 |
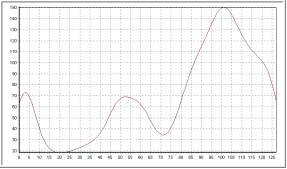 |
| Varianza 5 |
 |
 |
 |
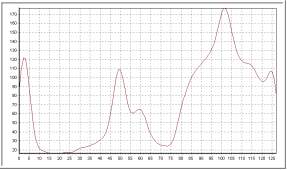 |
| Varianza 1 |
 |
 |
 |
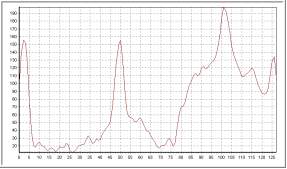 |
Dependiendo de la varianza del kérnel se obtiene un nivel de suavizado distinto,
a mayor varianza mayor suavizado. El problema es encontrar un equilibrio entre el
nivel de suavizado y el nivel de preservación de bordes, a mayor varianza, menor
preservación.
Kérnel de caja
| * |
Kérnel |
Convolución |
Renglón 64 (antes de convolución) |
Renglón 64 (después de convolución) |
| Tamaño 15 |
 |
 |
 |
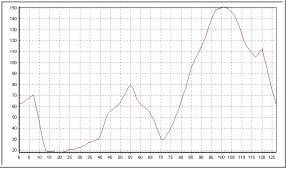 |
| Tamaño 7 |
 |
 |
 |
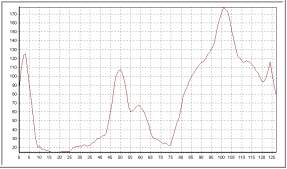 |
| Tamaño 3 |
 |
 |
 |
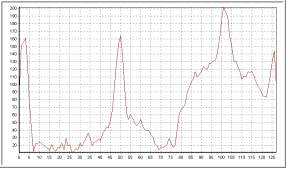 |
Este kérnel es más sensible a saltos bruscos de la señal en la vecindad de cada
pixel, esto se debe a que el kérnel da el mismo peso a toda la vecindad de cada pixel de la
señal original. Ésto se observa en los picos que se forman al suavizar, ésto no
ocurre con el kérnel gaussiano, que es más suave.
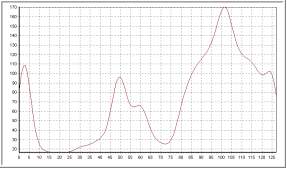
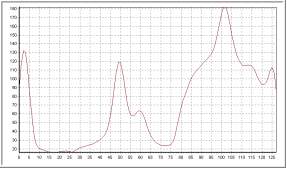
Kérnel binomial
| * |
Kérnel |
Convolución |
Renglón 64 (antes de convolución) |
Renglón 64 (después de convolución) |
| Orden 15 |
 |
 |
 |
 |
| Orden 7 |
 |
 |
 |
 |
| Orden 3 |
 |
 |
 |
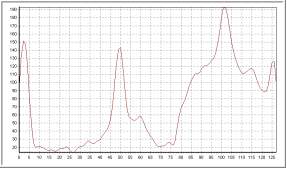 |
Como ya habíamos visto, el kernel binomial aproxima al kérnel gaussiano; los
resultados son muy parecidos a los obtenidos con el gaussiano.
Un par de kérneles en color...
Imagen original

Ejercicios. Página 54.
1) Calcule manualmente (por convolución repetida con (1,1)) los operadores
binomiales en 1-D de orden 2,3,4, y 5.
Bueno, también hace falta decir qué significa "(1,1)", si es una señal de
longitud 2 que empieza en 0 entonces, usando el triángulo de Pascal, obtenemos:
| orden\x |
0 | 1 | 2 | 3 | 4 | 5 |
| 0 |
1 | 0 | 0 | 0 | 0 | 0 |
| 1 |
1 | 1 | 0 | 0 | 0 | 0 |
| 2 |
1 | 2 | 1 | 0 | 0 | 0 |
| 3 |
1 | 3 | 3 | 1 | 0 | 0 |
| 4 |
1 | 4 | 6 | 4 | 1 | 0 |
| 5 |
1 | 5 | 10 | 10 | 5 | 1 |
Hay que observar que la sucesión no nula empieza en 0 y se extiende para x positiva..., Si
consideramos que "(1,1)" es una señal que empieza en -1, entonces la sucesión
se extiende para x negativa... pero lo que queremos es que se extienda en ambos sentidos,
lo que hay que hacer es alternar el kérnel, primero basado en 0 y luego basado en -1,
así, comenzando en 0 tenemos:
| orden\x |
-2 | -1 | 0 | 1 | 2 | 3 |
| 0 |
0 | 0 | 1 | 0 | 0 | 0 |
| 1 |
0 | 0 | 1 | 1 | 0 | 0 |
| 2 |
0 | 1 | 2 | 1 | 0 | 0 |
| 3 |
0 | 1 | 3 | 3 | 1 | 0 |
| 4 |
1 | 4 | 6 | 4 | 1 | 0 |
| 5 |
1 | 5 | 10 | 10 | 5 | 1 |
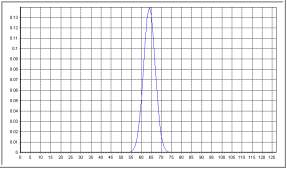
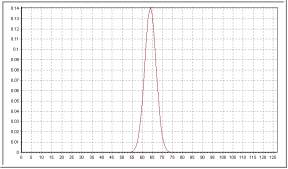
2) Grafique usando Calimán el kernel binomial de orden 17. ¿ Cuál será el
parámetro sigma del kernel Gaussiano que lo aproxima ? Grafique este kernel.
| Kérnel binomial de orden 16 |
Kérnel gaussiano ajustado |
 |
 |
A continuación muestro el algoritmo en CALIMÁN para obtener el parámetro:
imag(1) = impulso(1,128,0,64)
imag(2) = suavbinom(imag(1),16) //Por alguna razón CALIMÁN no me permitió generar el kérnel de orden 17...
imag(2) = imag(2) / 0.139949902892113 //Ese número es la "sumatoria" de la imagen 2 (hacemos que imag(2) sea función de densidad)
imag(3) = rampax(1,128,1.0)
imag(3) = imag(3) - 64
imag(4) = pow2(imag(3)) //Estoy usando el hecho de que la media de la func. de densidad es 0
imag(5) = imag(2) * imag(4) //La "sumatoria" de imag(5) es ahora la varianza de la función de densidad que construimos
imag(6) = suavgauss(imag(1),2.82842707633)//Ese número es justamente la raiz de la "sumatoria" de imag(5) (desviación estándard de la func. de densidad.)
imag(6) = imag(6) / 0.141053602099419 //Forzamos a que imag(6) sea función de densidad
imag(7) = imag(2) - imag(6) //La diferencia entre ambas funciones de densidad debe ser casi nula(y en efecto lo es)
Bueno, CALIMÁN falló al calcular el kérnel binomial de orden 17, entonces hice el
ejercicio para el kérnel de orden 16. El parámetro que nos piden es entonces 2.828427.
Ejercicios. Página 55.
1) Verifique que (1,-1) es un diferenciador numérico, generándolo con el botón
/derivadas/conv[7,7] de Calimán y aplicándolo a:
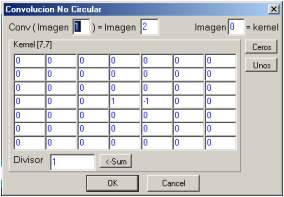 a) una rampa
a) una rampa
Se trata de un derivador "hacia atrás", i.e., utiliza la aproximación f(x)-f(x-1),
la imagen convolucionada es constante con valor 1(excepto la primera columna, donde el operador
no está definido), como se esperaba:
 b) una cuadrática
b) una cuadrática
En la imagen no se aprecia fácilmente la forma de la derivada... aquí está la gráfica:
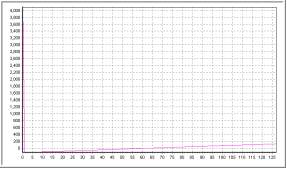
Como se esperaba, se trata de una recta de pendiente distinta de cero. La "cuadrática" que utilicé
fue (x-64)^2:
imag(1) = rampax(128,128,1.0)
imag(2) = imag(1) - 64
imag(3) = pow2(imag(2))
b) una cúbica:
En la imagen no se aprecia fácilmente la forma de la derivada... aquí está la gráfica:
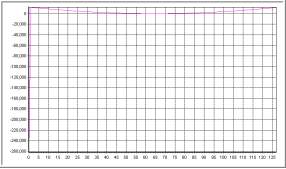
Como se esperaba, se trata de la gráfica de una cuadrática. La cúbica que usé es(x-64)^3:
imag(1) = rampax(128,128,1.0)
imag(2) = imag(1) - 64
imag(3) = pow(imag(2),3)
d)una Gaussiana
En la imagen no se aprecia fácilmente la forma de la derivada... aquí está la gráfica:
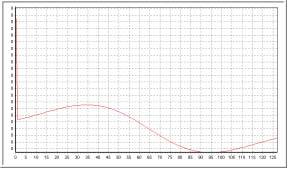
Así generé la gaussiana:
imag(1) = rampax(128,128,1.0)
imag(1) = impulso(128,128,64,64)
imag(2) = suavgauss(imag(1),30)
Usando el derivador de CALIMÁN, la gráfica de la derivada queda como:
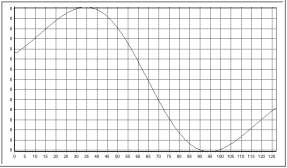
La diferencia en la apariencia se debe al cambio de escala que se hace por la primera columna.
Ejercicios. Página 56.
1) Demuestre, usando las propiedades dela convolución, que aplicar el
operador de derivada Gaussiana es equivalente a derivar la señal previamente
suavizada con un kernel Gaussiano de la misma sigma.

2) Demuestre la propiedad anterior en forma numérica usando Calimán.
| Imagen original |
Imagen original suavizada |
Derivada de la imagen suavizada |
Derivada gaussiana de la imagen original |
 |
 |
 |
 |
imag(2) = impulso(128,128,64,64)
imag(2) = suavgauss(imag(2),10)
imag(3) = dxatras(imag(2)) //imag(3)=kernel de derivada gaussiana
imag(4) = convolucion(imag(1),imag(3)) //imag(4) Derivada gaussiana de imag(1)
imag(5) = convolucion(imag(1),imag(2)) imag(5)= imag(1) suavizada
imag(6) = dxatras(imag(5)) imag(6)= derivada de la imagen suavizada
imag(7) = imag(4) - imag(6) La diferencia de estas dos imágenes es casi cero...
Ejercicios. Página 58.
1) La aproximación por diferencias finitas a la primera derivada es la primera
diferencia: f’(x) = f(x) - f(x-1). Empleando este esquema, indique cuales son
las aproximaciones en 2-D al gradiente, a la magnitud del gradiente y al
Laplaciano. ¿ Cuales de estos operadores son lineales ? ¿ Cuales son los
kerneles de convolución correspondientes ?
La aproximación al gradiente debe ser un par de imágenes que corresponden a las derivadas parciales
aproximadas por separado, esto es, las señales g y h dadas por:
g(x,y)=f(x,y)-f(x-1,y)//derivada parcial de f respecto a x
h(x,y)=f(x,y)-f(x,y-1)//derivada parcial de f respecto a y
La aproximación a la magnitud del gradiente debe ser:
sqrt(g^2 + h^2)//La magnitud del vector (f(x,y),g(x,y))
La aproximación a la segunda derivada de f(x) es f(x-1)-2f(x)+f(x+1), entonces la aproximación
al laplaciano debe ser:
L(x,y)=(f(x-1,y)-2f(x,y)+f(x+1,y)) + (f(x,y-1)-2f(x,y)+f(x,y+1))
O sea que el kernel de convolución para el Laplaciano es justamente:
y bueno!, el kérnel de derivación es simplemente (1,-1), el cual se aplica por
separado para obtener el gradiente.
Ya sabemos que tanto el gradiente como el laplaciano son operadores lineales invariantes bajo
traslación. Sin embargo, el operador "magnitud del gradiente" no es lineal, involucra
operadores cuadráticos sobre sus argumentos.
Ejercicios. Página 59.
1) Las diferencias entre 2 suavizadores a distintas escalas indican el detalle
perdido alpasar de una escala a otra. Para una imagen de prueba, calcule las
diferencias entre los resultados de los suavizadores con sigmas 1 y 2. ¿ Que
indica el valor absoluto de esta diferencia ?
| Imagen original |
Suavizada con s=1 |
Suavizada con s=2 |
Diferencia |
Abs(Diferencia) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
El valor absoluto de la diferencia indica la magnitud del detalle perdido al pasar de
una escala a otra. Una imagen casi "negra" como resultado indica poca diferencia entre el
desempeño de ambos suavizadores(son casi iguales). Intuitivamente, en los bordes
es donde debe haber mayor diferencia, ya que un suavizador con mayor varianza destruye
más fácilmente los bordes, mientras que uno con poca varianza los preserva.
Ejercicios. Página 60.
1) Construya, usando Calimán, un detector de bordes aplicando un umbral a la
magnitud del gradiente Gaussiano de una imagen. Este detector tiene 2
parámetros: el parámetro de escala sigma y el umbral u. Experimente con
diferentes valores de estos parámetros en al menos 2 imágenes diferentes.
Código (CALIMÁN):
imag(2) = maggradg(imag(1),1)
imag(3) = umbral(imag(2),0.001905906,7.729759)
imag(4) = umbral(imag(2),0.001905906,15.45761)
imag(5) = umbral(imag(2),0.001905906,23.18547)
imag(6) = umbral(imag(2),0.001905906,30.91332)
imag(7) = umbral(imag(2),0.001905906,38.64117)
| * |
|gradiente| |
Umbral al 10% |
Umbral al 20% |
Umbral al 30% |
Umbral al 40% |
Umbral al 50% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
| * |
|gradiente| |
Umbral al 10% |
Umbral al 20% |
Umbral al 30% |
Umbral al 40% |
Umbral al 50% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
Los bordes que se obtienen son demasiado gruesos para varianzas grandes, pero también se obtienen
discontinuidades para varianzas pequeñas. No es un buen detector de bordes.
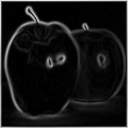
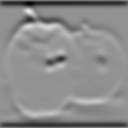
2) Otro detector de bordes puede construirse encontrando los cruces por cero
del Laplaciano Gaussiano de una imagen. En este caso se tiene sólo el
parámetro sigma. Repita los experimentos del ejercicio 1 con este detector
para doferentes valores de sigma.
Código (CALIMÁN):
imag(2) = d2xgauss(imag(1),1)
imag(3) = d2ygauss(imag(1),1)
imag(4) = imag(2) + imag(3)
imag(5) = crucex0(imag(4))
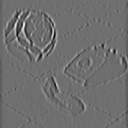
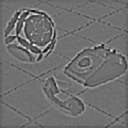
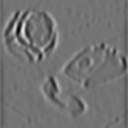
| * |
2a. derivada x |
2a. derivada y |
Laplaciano |
Cruces por cero |
| sigma=1 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
| * |
2a. derivada x |
2a. derivada y |
Laplaciano |
Cruces por cero |
| sigma=1 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
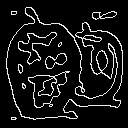 |
Este método es demasiado sensible al ruido, es fácil que los bordes de los
objetos se confundan con su textura.
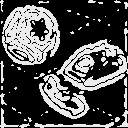
3) En lugar de cruces por cero,onstruya una imagen que valga 0 si el valor
absoluto del laplaciano es menor que cierto umbral, y 1 de otro modo.
Experimente con distintos umbrales.
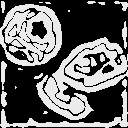
| * |
Laplaciano |
Abs(Laplaciano) |
Umbral al 5% |
Umbral al 10% |
Umbral al 15% |
Umbral al 20% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
| * |
Laplaciano |
Abs(Laplaciano) |
Umbral al 5% |
Umbral al 10% |
Umbral al 15% |
Umbral al 20% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
Estos bordes son de muy mala calidad, pero se observa algo interesante: aproximadamente en
el centro de lo que se reporta como borde hay una linea delgada muy bien definida que
recorre el contorno de los objetos... esta linea corresponde al cruce por cero del laplaciano de
la imagen; después de observar ésto da la sensación de que el método
de combinar el detector de "cruce por cero del laplaciano" con "magnitud del gradiente", puede
funcionar bastante bien.
4) Añada ruido Gaussiano a las imágenes de los ejercicios anteriores y repita
los experimentos. Comente sobre el desempeño de estos detectores y sobre los
valores de los parámetros.
| * |
|gradiente| |
Umbral al 10% |
Umbral al 20% |
Umbral al 30% |
Umbral al 40% |
Umbral al 50% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
| * |
|gradiente| |
Umbral al 10% |
Umbral al 20% |
Umbral al 30% |
Umbral al 40% |
Umbral al 50% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
Este detector de bordes no es demasiado sensible al ruido si elegimos apropiadamente la varianza
del suavizador... los resultados son muy similares a los obtenidos sin ruido.
| * |
2a. derivada x |
2a. derivada y |
Laplaciano |
Cruces por cero |
| sigma=1 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
| * |
2a. derivada x |
2a. derivada y |
Laplaciano |
Cruces por cero |
| sigma=1 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
En este caso, el ruido practicamente destruyó los bordes. Es necesario aplicar un
suavizador demasiado fuerte para evitar que el ruido afecte demasiado pero claramente un
suavizador muy fuerte de hecho destruye los bordes...
| * |
Laplaciano |
Abs(Laplaciano) |
Umbral al 5% |
Umbral al 10% |
Umbral al 15% |
Umbral al 20% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
| * |
Laplaciano |
Abs(Laplaciano) |
Umbral al 5% |
Umbral al 10% |
Umbral al 15% |
Umbral al 20% |
| sigma=1 |
 |
 |
 |
 |
 |
 |
| sigma=2 |
 |
 |
 |
 |
 |
 |
| sigma=3 |
 |
 |
 |
 |
 |
 |
Basta ver estas imágenes para darnos cuenta de que este suavizador es muy pobre...sin
importar el nivel de suavización.