DEFINICION: Sea J Ì
Â2 un nudo y sea I la parte
de adentro de J. Si s es un triángulo
de una descomposición en triángulos de [`I]
tal que sÇJ ¹
Æ, diremos que s
es un triángulo libre de [`I] si y sólo
si sÇJ es exactamente una arista de s
o es exactamente dos aristas de s.
LEMA: Si [`I] está descompuesto
en al menos dos triángulos, entonces existen al menos dos triángulos
libres.
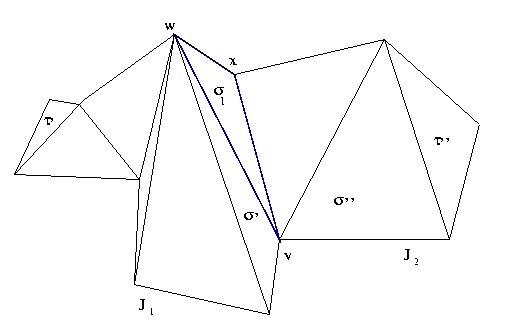
DEMOSTRACION: Supongamos que [`I] = s1È...Èsk donde si es un triángulo y Çsj es o bien vacío, o bien un vértice común, o bien una arista común para i ¹ j; i,j = 1,...,k. Esta demostración la haremos por inducción sobre k. Supongamos que k = 2, entonces tanto como s1 como s2 son libres. Por el hecho de que J es nudo en Â2 y las hipótesis antes mencionadas. Supongamos entonces que para cualquier nudo, en el cual su interior está descompuesto en al menos dos triángulos y menos de k triángulos, se cumple el lema. Demostrémoslo ahora para un nudo cuyo interior está dividido en k triángulos, es fácil ver que existen al menos dos triángulos cuya intersección con J es exactamente una arista, si los dos son libres, ya acabamos; Si al menos uno, no lo es, entonces el otro triángulo, digamos sl, donde l está fijo, interseca a J en una arista e de sl y en un vértice v de sl tal que v Ï e. Digamos que e = < w,x >

Los vértices de sl descomponen a J en dos arcos poligonales J1 y J2. Digamos que J1Çsl = < v,w > y que J2Çsl = < v,x > ; luego J¢ = J1È < v,w > y J¢¢ = J2È < v,x > son nudos cuyas partes de adentro están descompuestas en triángulos en una cantidad menor que k. No puede suceder que no haya triángulos en J¢ o en J¢¢, de lo contrario sl sería libre en [`I]. Si, digamos, dentro de J¢ sólo hay un triángulo t, entonces t es triángulo libre de [`I]. Así podemos suponer que dentro de J¢ y J¢¢ hay al menos dos triángulos (y hay menos de k triángulos). Por hipótesis de inducción en la parte de adentro de J¢ hay dos triángulos libres s' y t', y en la parte de adentro de J¢¢ hay dos triángulos libres s'' y t''. Podemos suponer que t' y t'' están "lejos" de sl (o sea que no comparten una arista de sl, porque entonces serían triángulos libres de J¢ y de J¢¢, respectivamente, y eso no es precisamente lo que queremos) así las cosas, resulta que t'y t'' son libres en [`I].
|
Siguiente | 
|