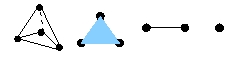
Trataremos de explicar todo esto de categoria PL. Para esto tenemos que ver varios conceptos: simplejos, caras y complejos simpliciales.

DEFINICION: Sean {x₀,x₁,...,x_n} Ì Â^k. Se dice que {x₀,x₁,...,x_n} estan en posición general ssi {x₁-x₀,x₂-x₀,...,x_n-x₀} es linealmente independiente.

DEFINICION: Sean {x₀,x₁,...,x_n} Ì Â^k puntos en posición general. Definimos el n-simplejo generado por {x₀,x₁,...,x_n} denotado por < x₀,x₁,...,x_n > de la siguiente manera

esto se ve como en la siguiente figura:

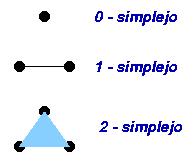
DEFINICION: Sea s = < x₀,x₁,...,x_n > un n-simplejo en Â^k y sea g Ì {x₀,x₁,...,x_n}. Entonces, decimos que t = < g > es una cara de s de dimensión #g- 1 y lo denotamos por t<s

Por ejemplo, un 2 - simplejo tiene las siguientes caras:

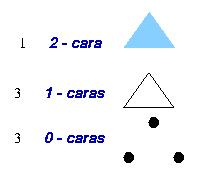
DEFINICION: Sea M un conjunto de simplejos en Â^k,entonces M se llama un complejo simplicial ssi sucede lo siguiente:

i)Si s Î M& t< s Þt Î M

ii) Si s,t Î M Þ sÇt<s Ù sÇt<t

iii) "s Î M,$U abierto en Â^k, tal que s Ì U y U intersecta sólo a un número finito de elementos de M.

DEFINICION: |M| = È_{s Î M}s se llama la realización de M y se dice que |M| es un poliedro.

Ejemplos.

1. La recta y el plano son complejos simpliciales.
2. Este no es un complejo simplicial, ya que auque la podemos ver como formado por 2-simplejos, tiene un punto de acumulación A, es decir, falla la propiedad iii)

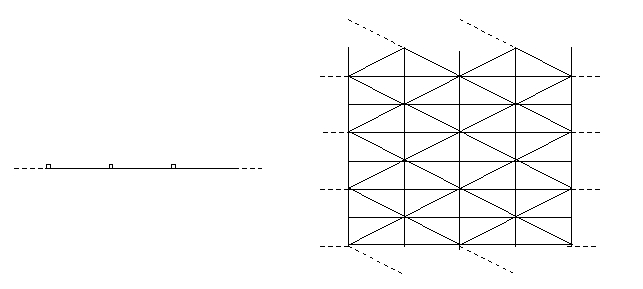
Ahora si ya podemos definir las funciones que nos interesan.

Regresar a Introducción

Siguiente

Página principal