• Manual de la librería.
• Instalación y prueba en Windows .
• Instalación y prueba en Ubuntu .
• Ejemplos .

 

Instalación y prueba de la librería GSL en Windows

1. Descargar codeblocks-10.05mingw-setup.exe, para instalar la versión de Code::Blocks que incluye MinGW .
2. Descargar los archivos de GSL para MinGW. Descompactar el archivo Zip dentro de del directorio c:\Program Files\CodeBlocks\MinGW\, cuidando que los archivos queden distribuidos en los directorios correspondientes (include, lib, bin y share).
3. Crear una aplicación de consola en Code::Blocks .
4. Ir la archivo main.cpp y copiar este código para generar numeros pseudo-aletorios con distribución normal ( (ver la descripción del programa).
5. Seleccionar la opción Linker settings de la ventana Project -> Build options.
   
   
   
   
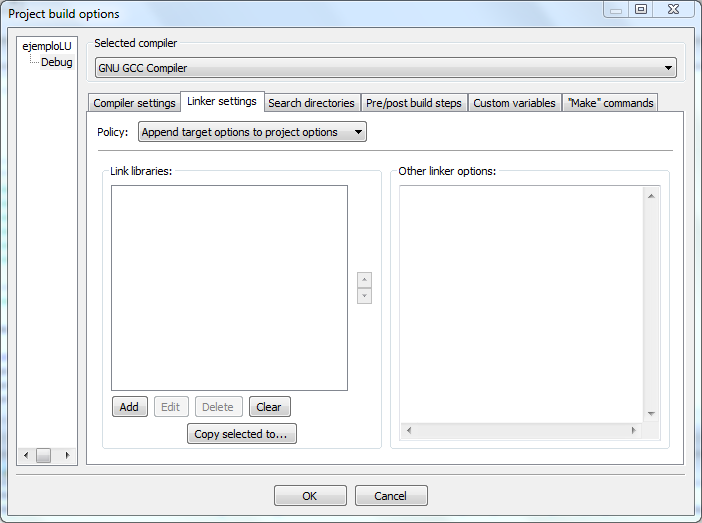
6. Presionar el botón Add para que aparezca la ventana:
   
   
   
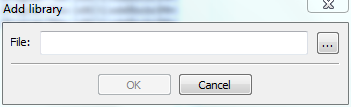
   Seleccionar el botón para buscar el archivo e ir a c:\Program Files\CodeBlocks\MinGW\lib y seleccionar libgsl.a.
   
   
   
   
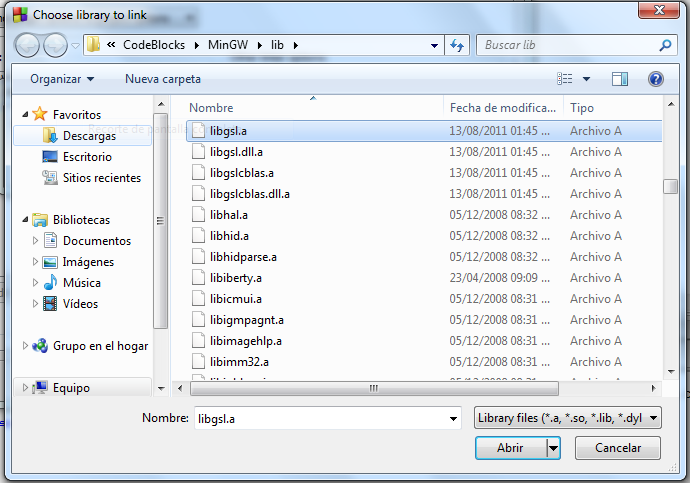
7. Repetir el paso anterior para incluir las librerías libgslcblas.a y libm.a.
8. Ver la descripción del programa para ejecutarlo.

 

Instalación y prueba de la librería GSL en Ubuntu

• Instalar con Synaptic o apt-get el paquete libgsl0ldbl y libgsl0-dev.
• Para compilar el programa randomNormal.c desde la línea de comandos, ejecutar la instrucción desde una consola:
  
  gcc -o randomNormal randomNormal.c -lgsl -lgslcblas -lm
  
  
• Ver la descripción del programa para ejecutarlo.
• Para compilar el programa usando Code::Blocks, repetir los pasos 3-8 de la sección "Instalación y prueba de la librería GSL en Windows". La diferencia es la ruta en la que se encuentran los archivos, los cuales deben estar en /usr/lib/

 

Ejemplos usando GSL

• Representación de los números de máquina de acuerdo al formato de la IEEE y formas de redondeo.
  Código  |  Descripción .
• Cálculo de la aproximación de log(2) por medio de una serie, usando tres formas de redondeo.
  Código  |  Descripción .
• Generador de números aleatorios con distribución normal.
  Código  |  Descripción .
• Lectura y escritura de un archivo con los elementos de un arreglo 1D.
  Código  |  Descripción .
• Lectura y escritura de un archivo con los elementos de un arreglo 2D.
  Código 1  |  Código 2  |  Descripción .