Eliminación Gaussiana simple.

    Este método se aplica para resolver sistemas lineales de la forma: A*X = B. Consiste en escalonar la matriz aumentada del sistema aumentado

para obtener un sistema equivalente:

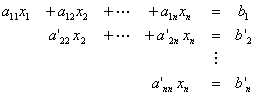
donde la notación se usa simplemente para denotar que el elemento cambió.    Se despejan las incógnitas comenzando con la última ecuación y hacia arriba.    Por  esta  razón,  muchas  veces  se  dice  que  el  método  de eliminación Gaussiana consiste en la eliminación hacia adelante y sustitución hacia atrás.

Desventajas:

1. División entre cero. Una de sus desventajas es que durante el proceso en las fases de eliminación y sustitución es posible que ocurra una división entre cero. Se ha desarrollado una estrategia del pivoteo para evitar parcialmente estos problemas. Ésta se deja como investigación al alumno.

    

2. Errores de redondeo. La computadora maneja las fracciones en forma decimal con cierto número limitado de cifras decimales, y al manejar fracciones que se transforman a decimales que nunca terminan, se introduce un error en la solución de la computadora. Este se llama error por redondeo.

   Cuando se va a resolver solamente un pequeño número de ecuaciones, el error por redondeo es pequeño y generalmente no se afecta sustancialmente la presición de los resultados, pero si se van a resolver simultáneamente muchas ecuaciones, el efecto acumulativo del error por redondeo puede introducir errores relativamente grandes en la solución. Por esta razón el número de ecuaciones simultáneas que se puede resolver satisfactoriamente con el método de eliminación de Gauss, utilizando de 8 a 10 dígitos significativos en las operaciones aritméticas, se limita generalmente a 15 o 20.

    

3. Sistemas mal condicionados. La obtención de la solución depende de la condición del sistema. En sentido matemático, los sistemas bien condicionados son aquellos en los que un cambio en uno o más coeficientes provoca un cambio similar en la solución. Los sistemas mal condicionados son aquellos en los que cambios pequeños en los coeficientes provocan cambios grandes en la solución.

   Una interpretación diferente del mal condicionamiento es que un rango amplio de respuestas puede satisfacer aproximadamente al sistema. Ya que los errores de redondeo pueden inducir cambios pequeños en los coeficientes, estos cambios artificiales pueden generar errores grandes en la solución de sistemas mal condicionados.

Para evitar todos estos inconvenientes trabajamos con la estrategia de pivoteo (parcial o total).

Seudocodigo del algoritmo