Superficies

Actividad	Proyecto	Descripción
1	Trisección del cubo
1	Copa	Superficies de revolución
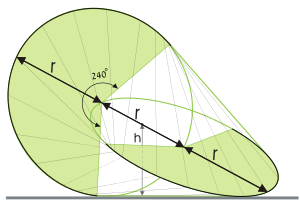
2	Oloide	El oloide es un cuerpo geométrico tridimensional creado por Paul Schatz en 1929. Consiste en la envolvente convexa de una estructura construida colocando dos círculos de mismo radio y enlazados en planos perpendiculares, de forma que el centro de cada círculo reside sobre el borde del otro. Wikipedia
3	Esfericones	El esfericón es un cuerpo geométrico que posee una única cara, dos aristas y cuatro vértices. Fue introducido por primera vez por el inventor de juegos y juguetes israelí David Haran Hirsch, quien lo patentó en Israel en 1980. Su nombre le fue dado por el inglés Colin Roberts, quien también lo exploró. En 1999 su descubrimiento llamó la atención de Ian Stewart que más tarde publicó un artículo sobre el mismo en la revista Scientific American. La curva suave de la costura de una pelota de tenis queda determinada por el contacto de una esfera inscrita a un esfericón. Wikipedia Es posible construir diferentes sólidos pertenecientes a la familia del esfericón y clasificarlos en función del tipo de corte que posee la figura de revolución a partir de la cual se los genera. La manera de construirlos es la siguiente: Se divide un polígono regular de n lados por la mitad. Dependiendo del polígono el corte puede pasar por dos vértices (V-V), por un vértice y el punto medio de un lado (V-L) o por el punto medio de dos lados (L-L). A partir de la mitad obtenida se construye un sólido de revolución haciendo girar dicha mitad alrededor del eje a lo largo del cual se realizó el corte. Se divide el sólido de revolución por la mitad mediante un corte que pasa por el eje de simetría. Se rota una de las mitades en sentido horario en 360/i grados, con i=n,n-1,...,1
4	Superficies cuadráticas

Superficies

Proyectos