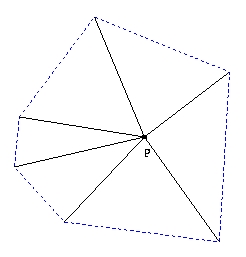
Empecemos haciendo la observación de que siempre podemos dividir el interior de un nudo, en triángulos de manera conveniente
TEOREMA: Sea J Ì Â2
un nudo y sea I la parte de adentro de J. Entonces la cerradura de la parte
de adentro [`I], es la unión de un número
finito de triángulos s1,...,sk
tales que siÇsj
es una cara común a ambos, para i ¹
j; i,j = 1,..k
Demostración: Observemos primero que si [`I] fuera convexo, escogiendo un punto p Î I, podemos trazar rectas de p a cada uno de los vértices de ¶[`I] = J. Esto descompone a [`I] en triángulos como se pide.

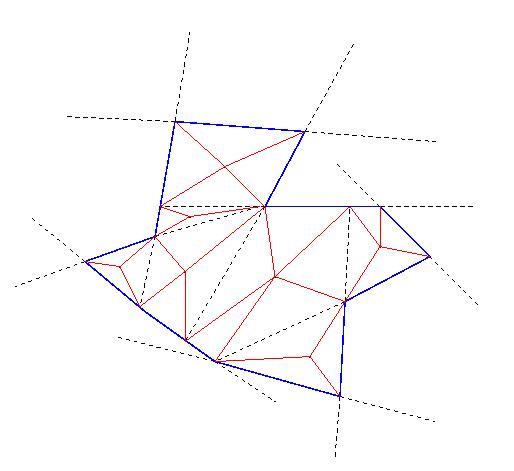
Si [`I] no es convexo, tomamos una recta Li por cada arista ei de J; de tal manera que ei Ì Li, donde J = e1È...Èer. Las rectas L1,...,Lr descomponen a Â2 en un número finito de subconjuntos convexos C1,...,Ct (esto se sigue de que una recta divide a Â2 en dos subconjuntos convexos y de que la intersección de convexos es convexo). Tenemos que [`I] es unión de algunos de estos convexos, digamos [`I] = C1È...ÈCl. A cada uno de estos convexos lo podemos triangular como antes y esto nos da una descomposición de [`I] en triángulos, tal como se pide.
DEFINICION: Sea u la arista de un nudo k en Â3 y sea D un triángulo en Â3 tal que ¶D = uÈvÈw (u, v y w son segmentos de recta). Si kÇD = u, entonces k¢ = (k-u)ÈuÈv define un nuevo nudo.
El tipo de triángulos de la definición anterior se llaman triángulos libres y se puede demostrar que siempre podemos escontrarlos,
|
|

|